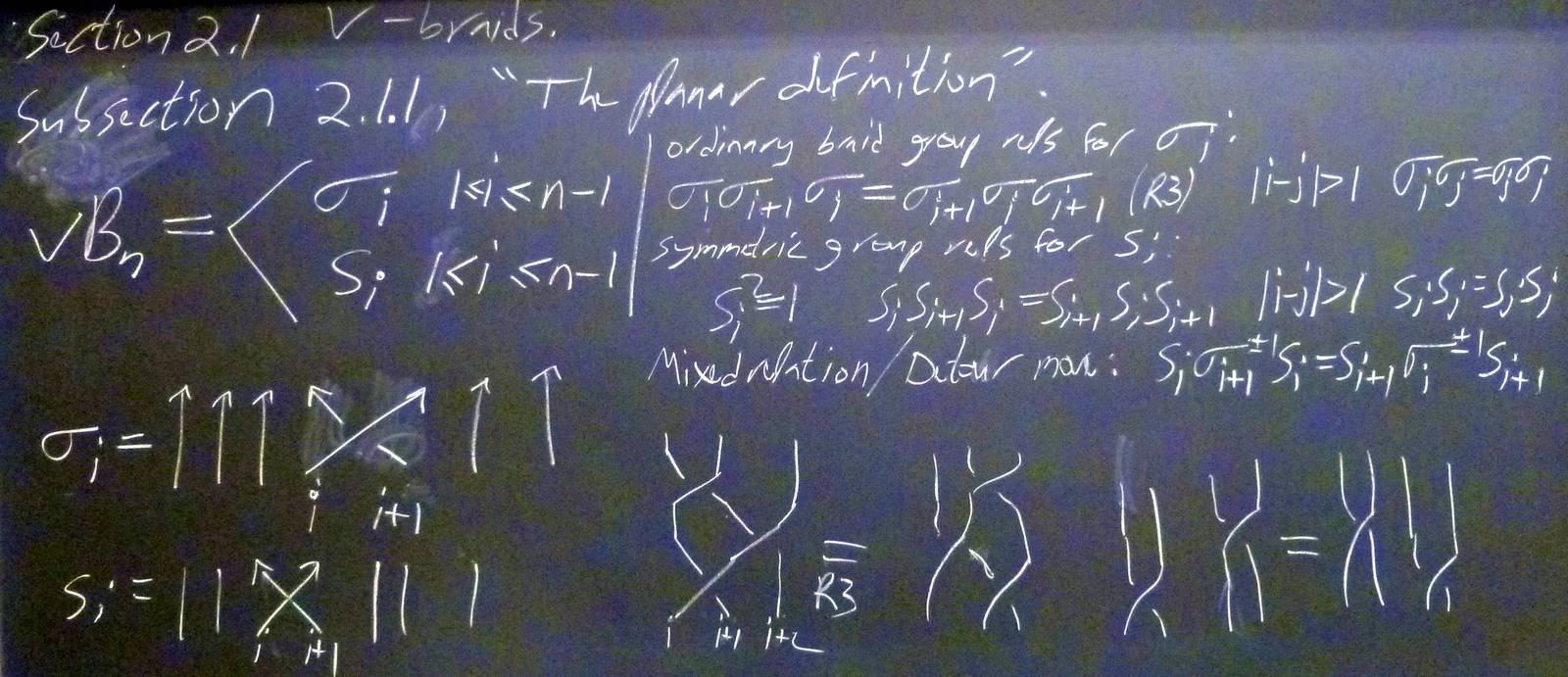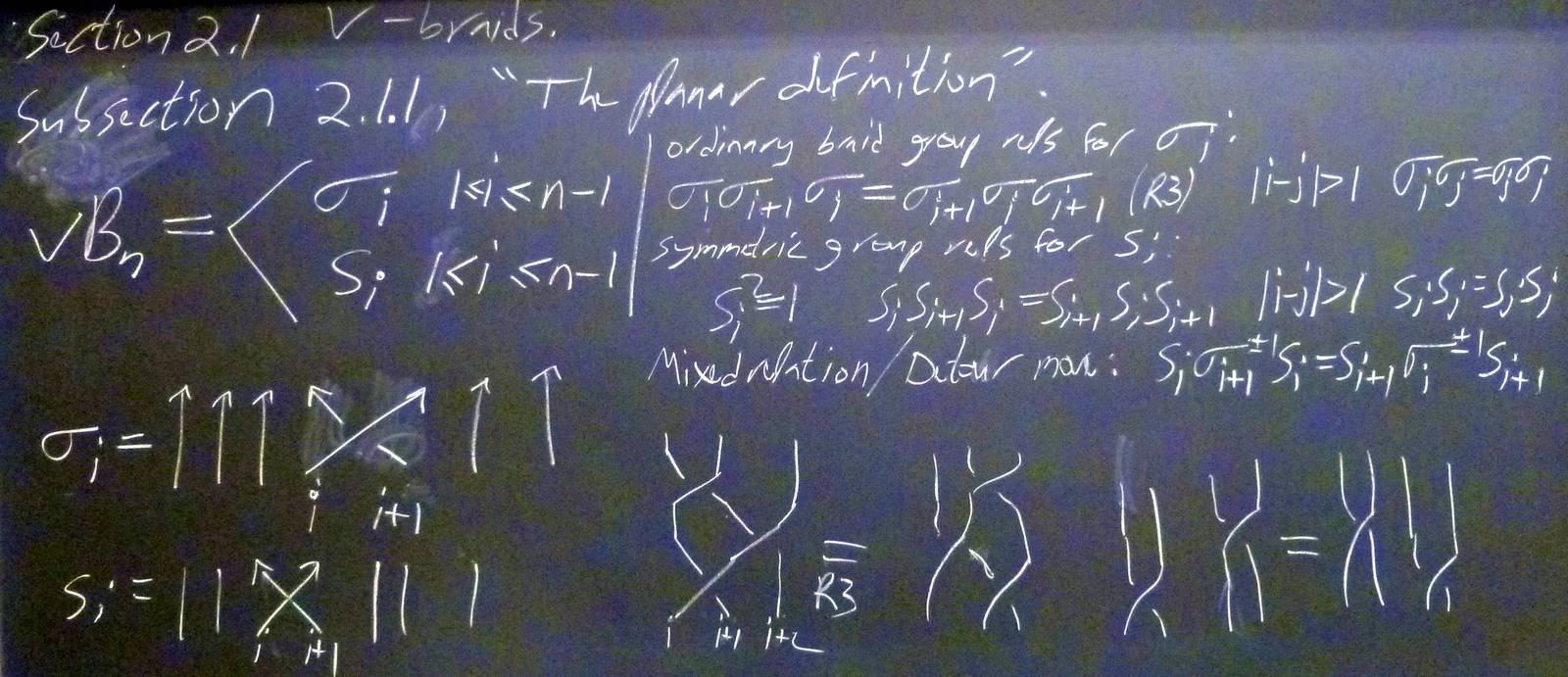
| wClips-{ | hide text |
| 120620-132027: | Future plans. |
| 120530-135829: | R3 as a composition of diffeomorphisms (2). |
| 120530-135516: | R3 as a composition of diffeomorphisms. |
| 120530-135145: | R as a diffeomorphism (2). |
| 120530-134642: | R as a diffeomorphism. |
| 120530-133843: | The adjoint and div (2). |
| 120530-133616: | The adjoint and div. |
| 120530-132304: | Verifying that the bracket goes to the commutator (2). |
| 120530-132037: | Verifying that the bracket goes to the commutator. |
| 120530-131156: | The tangential vector fields. |
| 120530-130716: | The map into differential operators. |
| 120530-125218: | Review of wheels, trees, div, and j. |
| 120523-135927: | div (3). |
| 120523-135531: | div (2). |
| 120523-134654: | div. |
| 120523-133943: | The splitting. |
| 120523-133509: | Comparing the brackets, more conceptually (2). |
| 120523-133050: | Comparing the brackets, more conceptually. |
| 120523-132729: | Comparing the brackets (5). |
| 120523-132320: | Comparing the brackets (4). |
| 120523-131621: | Comparing the brackets (3). |
| 120523-130834: | Comparing the brackets (2). |
| 120523-130329: | Comparing the brackets. |
| 120523-125831: | Primitives, wheels, and trees (4). |
| 120523-125534: | Primitives, wheels, and trees (3). |
| 120523-125424: | Primitives, wheels, and trees (2). |
| 120523-124956: | Primitives, wheels, and trees. |
| 120510-140700: | ${\mathcal A}^w$ and Alekseev-Torossian spaces (2). |
| 120510-135047: | Wheels and trees (2). |
| 120510-134619: | Wheels and trees. |
| 120510-134243: | Milnor-Moore and primitives. |
| 120510-133424: | ${\mathcal A}^w$ and Alekseev-Torossian spaces. |
| 120510-132343: | Proof of head invariance. |
| 120510-131406: | Bracket rise for w, head invariance. |
| 120510-130722: | Bracket rise for w. |
| 120510-130448: | v-Tangles, w-Tangles, their candidate projectivizations, and the w-expansion. |
| 120510-130052: | v-Tangles, w-Tangles, and their candidate projectivizations. |
| 120502-134819: | v-Tangles and w-Tangles. |
| 120502-134627: | Circuit Algebras with Skeleta. |
| 120502-133941: | Examples of Circuit Algebras (2). |
| 120502-133529: | Examples of Circuit Algebras. |
| 120502-132813: | Circuit Algebras. |
| 120502-132309: | Wiring diagrams (2). |
| 120502-131940: | Wiring diagrams. |
| 120502-131204: | Review of $\mathcal A$-Expansions (2). |
| 120502-130529: | Review of $\mathcal A$-Expansions. |
| 120502-130049: | Review of Expansions (3). |
| 120502-125327: | Review of Expansions (2). |
| 120502-125022: | Review of Expansions. |
| 120502-124716: | Review of Algebraic Structures. |
| 120425-140422: | Relations between $\Lambda$ and $Y$. |
| 120425-140058: | $\Lambda$. |
| 120425-135210: | The IAM Relations. |
| 120425-132710: | E(LHS). |
| 120425-130406: | E(RHS). |
| 120425-124359: | Dreams on an Alexander homology. |
| 120418-135500: | The BCH Formula (3). |
| 120418-134601: | The BCH Formula (2). |
| 120418-133856: | The Differential of the Exponential Function (3). |
| 120418-133226: | The Differential of the Exponential Function (2). |
| 120418-132328: | The Differential of the Exponential Function. |
| 120418-131408: | The BCH Formula. |
| 120418-130327: | The Euler Trick (3). |
| 120418-125634: | The Euler Trick (2). |
| 120418-125036: | The Euler Trick. |
| 120418-124645: | Detached wheels and hairy Y's. |
| 120418-124122: | Statement of the Alexander Theorem. |
| 120404-130233: | EZ. |
| 120404-125832: | The Euler operator. |
| 120404-125306: | Exercise 3.21: Detached wheels and hairy Y's. |
| 120404-124504: | Exercise 3.20: Commutators Commute. |
| 120404-123625: | A simplified version of the w-Alexander theorem. |
| 120404-122952: | The w-Alexander theorem (Theorem 3.27). |
| 120404-122243: | A classical formula for the Alexander polynomial. |
| 120404-120711: | A conjectured formula for the Alexander polynomial. |
| 120404-115926: | The trapping matrix. |
| 120404-115032: | What's $Z^w$ on knots? |
| 120328-152816: | Bicrossed scratch. |
| 120321-140025: | Homomorphic expansions. |
| 120321-135847: | Expansions. |
| 120321-135345: | Quandles and Leibniz algebras (5). |
| 120321-134725: | Quandles and Leibniz algebras (4). |
| 120321-133830: | Quandles and Leibniz algebras (3). |
| 120321-133421: | Quandles and Leibniz algebras (2). |
| 120321-132900: | Quandles and Leibniz algebras. |
| 120321-132356: | Quandles defined (2). |
| 120321-131614: | Quandles defined. |
| 120321-131212: | Groups and associative algebras. |
| 120321-130513: | Operations on proj. |
| 120321-130125: | ${\mathcal I}^m$ and the projectivization. |
| 120321-125146: | The augmentation ideal. |
| 120321-124643: | Examples - Actions, Quandles, QTGs, fibered situations. |
| 120321-124229: | Examples - groups and group homomorphisms. |
| 120321-123740: | Algebraic Structures. |
| 120314-140441: | The 2D example and ${\mathcal T}$ (2). |
| 120314-140017: | The 2D example and ${\mathcal T}$. |
| 120314-135504: | ${\mathcal T}$ descends to ${\mathcal A}^{wt}$ (4). |
| 120314-134812: | ${\mathcal T}$ descends to ${\mathcal A}^{wt}$ (3). |
| 120314-134227: | ${\mathcal T}$ descends to ${\mathcal A}^{wt}$ (2). |
| 120314-133959: | ${\mathcal T}$ descends to ${\mathcal A}^{wt}$. |
| 120314-133340: | The map ${\mathcal T}$. |
| 120314-132622: | The 2D example. |
| 120314-131943: | The co-commutative case. |
| 120314-131527: | The double is metrized (4). |
| 120314-130813: | The double is metrized (3). |
| 120314-130520: | The double is metrized (2). |
| 120314-130022: | The double is metrized. |
| 120314-125800: | What is $I{\mathfrak g}$? (2) |
| 120314-125144: | What is $I{\mathfrak g}$? |
| 120314-124450: | The tensor map claim. |
| 120314-123935: | ${\mathcal A}^w$ and ${\mathcal A}^{wt}$. |
| 120307-140335: | ${\mathcal A}^w(\bigcirc)$ (2). |
| 120307-135824: | ${\mathcal A}^w(\bigcirc)$. |
| 120307-135109: | Proof of bracket-rise (3). |
| 120307-134836: | Proof of bracket-rise (2). |
| 120307-134130: | Proof of bracket-rise. |
| 120307-132355: | Caravans of wheels and trees. |
| 120307-131928: | Wheels and trees. |
| 120307-130936: | The "bracket-rise" theorem. |
| 120307-130443: | ${\mathcal A}^{wt}$. |
| 120307-124327: | $Z^w$ is well-defined. |
| 120307-124140: | $Z^w$. |
| 120229-135002: | The Milnor-Moore theorem. |
| 120229-134612: | The product and the co-product. |
| 120229-134106: | ${\mathcal A}^{v,w}(\uparrow)$ and ${\mathcal A}^{v,w}(\bigcirc)$. |
| 120229-133825: | $\alpha:{\mathcal A}^u\to{\mathcal A}^v$. |
| 120229-133213: | 4T. |
| 120229-132915: | 6T. |
| 120229-132549: | ${\mathcal A}^{v,w}$. |
| 120229-132431: | Type $m$ invariants and their weight systems. |
| 120229-132021: | Semi-virtual crossings. |
| 120229-130442: | Framed and unframed long v-knots: proofs. |
| 120229-130311: | Framed and unframed long v-knots: the compositions. |
| 120229-125332: | Framed and unframed long v-knots: $h$. |
| 120229-124714: | Framed and unframed long v-knots: $\iota$ and $sl$. |
| 120229-124547: | Classical linkinf and self-linking numbers. |
| 120229-124517: | Framed and unframed long v-knots, day 2. |
| 120222-133119: | Framed and unframed long v-knots. |
| 120222-132410: | The self-linking numbers (2). |
| 120222-131844: | The self-linking numbers. |
| 120222-130333: | ${\mathcal K}^v$ is a non-Abelian monoid. |
| 120222-130027: | Long v-Knots and circular v-Knots. |
| 120222-125634: | u-Knots, v-Knots, w-Knots. |
| 120222-124827: | There's no $Z$ compatible with $\alpha$. |
| 120222-124329: | $\alpha:{\mathcal A}^u\to{\mathcal A}^w$. |
| 120215-140055: | 2.5.3 Uniqueness of a well-behaved homomorphic expansion. |
| 120215-135838: | 2.5.2 Injectivity; 2.5.3 Non-uniqueness in the non-homomorphic case. |
| 120215-135308: | 2.5.1.5 Compatibility with the action on the free group (2). |
| 120215-134523: | 2.5.1.5 Compatibility with the action on the free group. |
| 120215-133809: | 2.5.1.6 Non-compatability with strand doubling/unzipping. |
| 120215-133052: | 2.5.1.4 Compatibility with strand deletions (2). |
| 120215-132709: | 2.5.1.4 Compatibility with strand deletions. |
| 120215-132242: | 2.5.1.3 Compatibility with strand insertions. |
| 120215-131538: | The Magnus and the exponential expansions for the free group. |
| 120215-130448: | 2.5.1.2 Compatibility with braids cloning (2). |
| 120215-125912: | 2.5.1.2 Compatibility with braids cloning. |
| 120215-125131: | 2.5.1.1. Compatibility with braid invertion. |
| 120215-123443: | Review of $G\to{\mathcal A}^Q(G)$ and functoriality. |
| 120208-140123: | Checking R3 for $Z^w$. |
| 120208-135721: | uvw Table (5). |
| 120208-135214: | Expansions and homomorphic expansions. |
| 120208-134550: | Deriving 4T-Arrow. |
| 120208-134035: | Deriving 4T. |
| 120208-133640: | uvw Table (4). |
| 120208-133300: | Deriving locality and tails-commute. |
| 120208-132729: | Deriving the 6T relation. |
| 120208-131944: | uvw Table (3). |
| 120208-131634: | Generating $I^n/I^{n+1}$ (2). |
| 120208-130902: | Generating $I^n/I^{n+1}$. |
| 120208-130150: | Semi-virtuals crossings and their arrows. |
| 120208-125305: | Singular braids and chord diagrams. |
| 120208-124632: | uvw Table (2). |
| 120208-124221: | uvw Table. |
| 120201-140238: | Z^w. |
| 120201-135822: | Homomorphic QUFTI. |
| 120201-135630: | The fundamental theorem and QUFTI (3). |
| 120201-135220: | The fundamental theorem and QUFTI (2). |
| 120201-134536: | The fundamental theorem and QUFTI. |
| 120201-134345: | The "central" question of FTI. |
| 120201-133806: | QUFTI as filtered maps (2). |
| 120201-133441: | QUFTI as filtered maps. |
| 120201-133243: | gr is a functor. |
| 120201-132843: | Quadratic Universal Finite Type Invariant(s) (QUFTI). |
| 120201-132314: | A^w. |
| 120201-131843: | A^v. |
| 120201-131250: | 6T / CYB. |
| 120201-130713: | Quadratic relations. |
| 120201-130408: | Arrow diagrams (2). |
| 120201-130036: | Arrow diagrams. |
| 120201-125709: | What are the generators? What are the relations? |
| 120201-125045: | The PvBn case. |
| 120201-124604: | Type p invariants. |
| 120201-124249: | The augmentation ideal and its powers. |
| 120125-140415: | Chord diagrams for braids. |
| 120125-140131: | Chord diagrams for knots. |
| 120125-135825: | The top derivative is constant. |
| 120125-135010: | The definition of finite-type invariants. |
| 120125-134559: | Resolving double points. |
| 120125-132756: | The two actions of PvB_n (2). |
| 120125-132316: | The two actions of PvB_n. |
| 120125-131956: | No semi-direct structure in the w case. |
| 120125-131513: | The "u" case. |
| 120125-130948: | The action in the pure case. |
| 120125-130706: | The action on the product of all generators. |
| 120125-130211: | The action of real crossings (2). |
| 120125-130204: | The action of real crossings. |
| 120125-124729: | The action of virtual crossings. |
| 120125-124134: | Action by conjugation. |
| 120125-123642: | McCool's Theorem. |
| 120125-122827: | Artin's theorem. |
| 120118-135356: | A presentation with wens (2). |
| 120118-134845: | A presentation with wens. |
| 120118-133727: | Non-horizontal flying rings. |
| 120118-133344: | Ribbon singularities. |
| 120118-130809: | Horizontal flying rings as a fundamental group. |
| 120118-125803: | wB_n. |
| 120118-125435: | UC and OC. |
| 120118-125422: | The "\sigma_{ij}" presentation of PvB_n. |
| 120118-125101: | The "Yang-Baxter" relation. |
| 120118-124119: | v-Braids, again. |
| 120111-140241: | The wrong definition of uB_n is the right definition of vB_n. |
| 120111-135722: | vB_n as a semi-direct product with S_n. |
| 120111-134813: | Overcrossings don't commute and undercrossings don't commute. |
| 120111-133959: | The detour move. |
| 120111-133952: | vB_n. |
| 120111-130844: | A knot on a surface. |
| 120111-130836: | u, v, and w. |
| 120111-130829: | Topology, combinatorics, low algebra, high algebra. |
| } |
Notes for BBS/wClips-120111-133952.jpg: [edit]