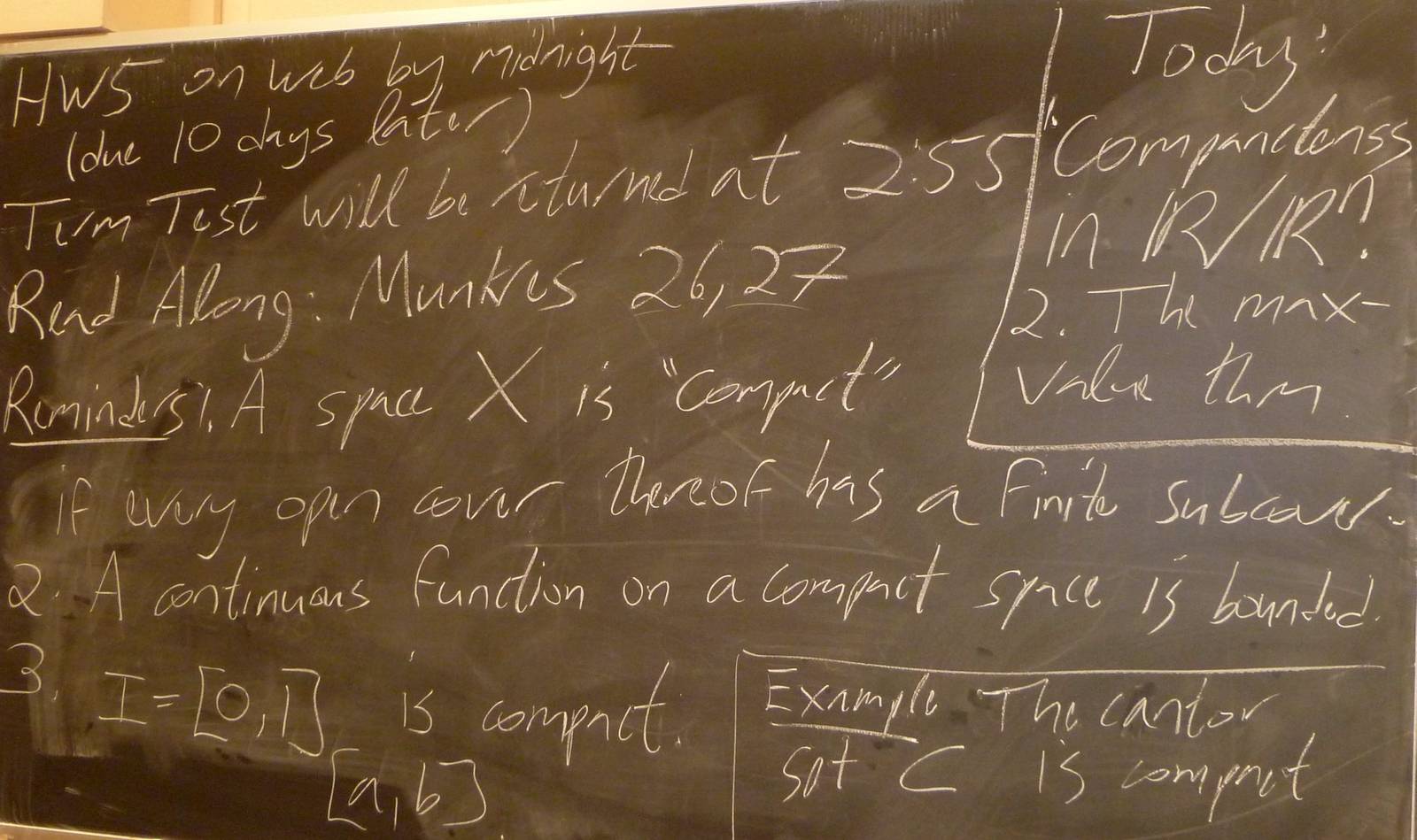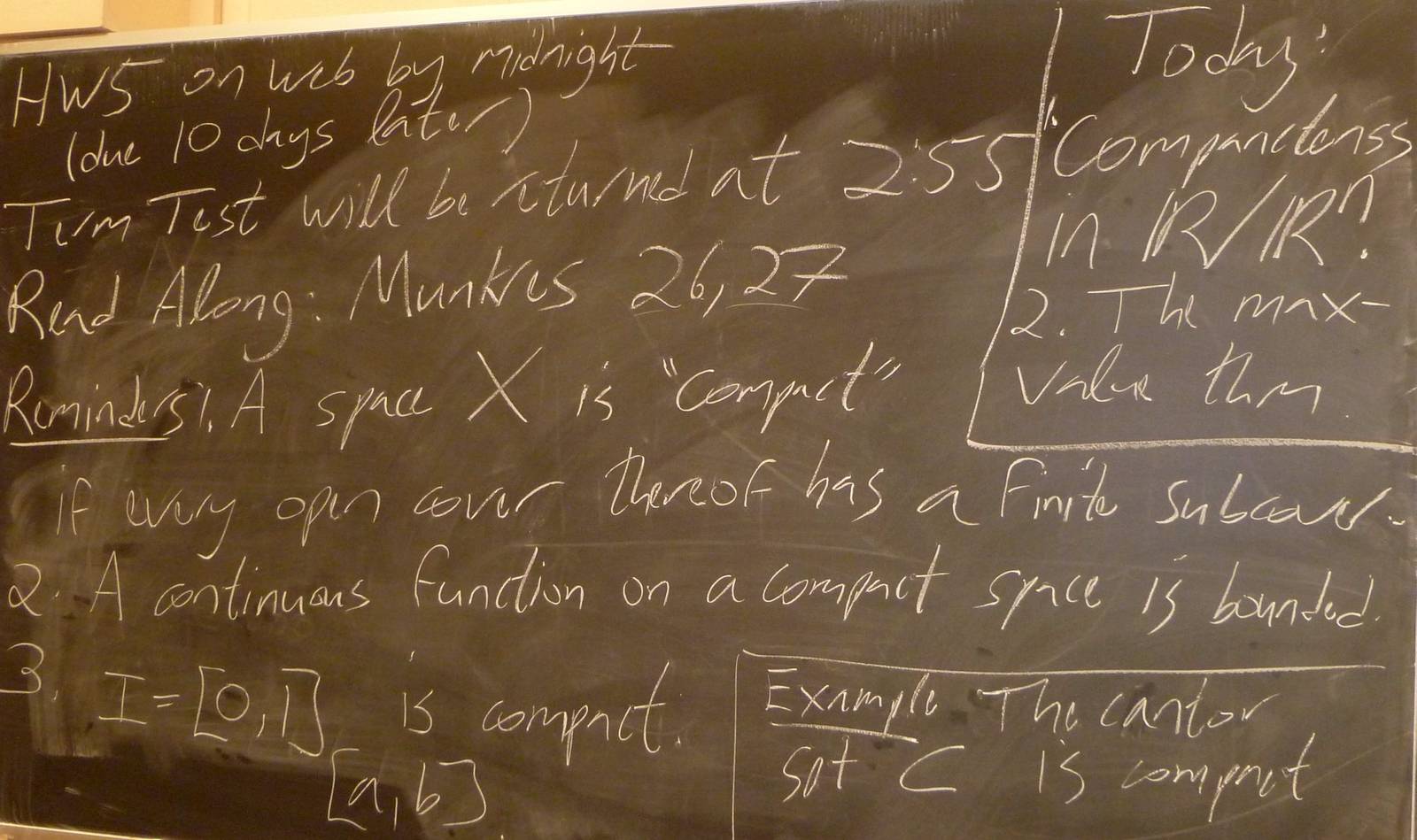
| 10_327-{ | hide text |
| 101206-150423: | Hour 35: Baire spaces and no-where differentiable functions (9). |
| 101206-150418: | Hour 35: Baire spaces and no-where differentiable functions (8). |
| 101206-150412: | Hour 35: Baire spaces and no-where differentiable functions (7). |
| 101206-144618: | Hour 35: Baire spaces and no-where differentiable functions (6). |
| 101206-144612: | Hour 35: Baire spaces and no-where differentiable functions (5). |
| 101206-144606: | Hour 35: Baire spaces and no-where differentiable functions (4). |
| 101206-142921: | Hour 35: Baire spaces and no-where differentiable functions (3). |
| 101206-142915: | Hour 35: Baire spaces and no-where differentiable functions (2). |
| 101206-142909: | Hour 35: Baire spaces and no-where differentiable functions. |
| 101202-154652: | Hours 33-34: Compactness and completeness (14). |
| 101202-154646: | Hours 33-34: Compactness and completeness (13). |
| 101202-153823: | Hours 33-34: Compactness and completeness (12). |
| 101202-153817: | Hours 33-34: Compactness and completeness (11). |
| 101202-153811: | Hours 33-34: Compactness and completeness (10). |
| 101202-151220: | Hours 33-34: Compactness and completeness (9). |
| 101202-151214: | Hours 33-34: Compactness and completeness (8). |
| 101202-145103: | Hours 33-34: Compactness and completeness (7). |
| 101202-145056: | Hours 33-34: Compactness and completeness (6). |
| 101202-145050: | Hours 33-34: Compactness and completeness (5). |
| 101202-144001: | Hours 33-34: Compactness and completeness (4). |
| 101202-143935: | Hours 33-34: Compactness and completeness (3). |
| 101202-142107: | Hours 33-34: Compactness and completeness (2). |
| 101202-142101: | Hours 33-34: Compactness and completeness. |
| 101129-150200: | Hour 32: Compactness in metric spaces (9). |
| 101129-150153: | Hour 32: Compactness in metric spaces (8). |
| 101129-150147: | Hour 32: Compactness in metric spaces (7). |
| 101129-144510: | Hour 32: Compactness in metric spaces (6). |
| 101129-144504: | Hour 32: Compactness in metric spaces (5). |
| 101129-144458: | Hour 32: Compactness in metric spaces (4). |
| 101129-142555: | Hour 32: Compactness in metric spaces (3). |
| 101129-142550: | Hour 32: Compactness in metric spaces (2). |
| 101129-142544: | Hour 32: Compactness in metric spaces. |
| 101125-155612: | Hours 30-31: Tietze's theorem (14). |
| 101125-155606: | Hours 30-31: Tietze's theorem (13). |
| 101125-155447: | Hours 30-31: Tietze's theorem (12). |
| 101125-153349: | Hours 30-31: Tietze's theorem (11). |
| 101125-153342: | Hours 30-31: Tietze's theorem (10). |
| 101125-153332: | Hours 30-31: Tietze's theorem (9). |
| 101125-151406: | Hours 30-31: Tietze's theorem (8). |
| 101125-151357: | Hours 30-31: Tietze's theorem (7). |
| 101125-144921: | Hours 30-31: Tietze's theorem (6). |
| 101125-144915: | Hours 30-31: Tietze's theorem (5). |
| 101125-144909: | Hours 30-31: Tietze's theorem (4). |
| 101125-142115: | Hours 30-31: Tietze's theorem (3). |
| 101125-142109: | Hours 30-31: Tietze's theorem (2). |
| 101125-142103: | Hours 30-31: Tietze's theorem. |
| 101125-131208: | A hint for HW7 problem 9. |
| 101122-150129: | Hour 29: A completely regular space is a subset of a cube (6). |
| 101122-150123: | Hour 29: A completely regular space is a subset of a cube (5). |
| 101122-150117: | Hour 29: A completely regular space is a subset of a cube (4). |
| 101122-143604: | Hour 29: A completely regular space is a subset of a cube (3). |
| 101122-143557: | Hour 29: A completely regular space is a subset of a cube (2). |
| 101122-143551: | Hour 29: A completely regular space is a subset of a cube. |
| 101118-160029: | Hours 27-28: Normal spaces and Urysohn's lemma (12). |
| 101118-160022: | Hours 27-28: Normal spaces and Urysohn's lemma (11). |
| 101118-160005: | Hours 27-28: Normal spaces and Urysohn's lemma (10). |
| 101118-151403: | Hours 27-28: Normal spaces and Urysohn's lemma (9). |
| 101118-151352: | Hours 27-28: Normal spaces and Urysohn's lemma (8). |
| 101118-144900: | Hours 27-28: Normal spaces and Urysohn's lemma (7). |
| 101118-144853: | Hours 27-28: Normal spaces and Urysohn's lemma (6). |
| 101118-143820: | Hours 27-28: Normal spaces and Urysohn's lemma (5). |
| 101118-143813: | Hours 27-28: Normal spaces and Urysohn's lemma (4). |
| 101118-142441: | Hours 27-28: Normal spaces and Urysohn's lemma (3). |
| 101118-142436: | Hours 27-28: Normal spaces and Urysohn's lemma (2). |
| 101118-142430: | Hours 27-28: Normal spaces and Urysohn's lemma. |
| 101115-150131: | Hour 26: Generalized limits (7). |
| 101115-145315: | Hour 26: Generalized limits (6). |
| 101115-145308: | Hour 26: Generalized limits (5). |
| 101115-145303: | Hour 26: Generalized limits (4). |
| 101115-143652: | Hour 26: Generalized limits (3). |
| 101115-143646: | Hour 26: Generalized limits (2). |
| 101115-143641: | Hour 26: Generalized limits. |
| 101111-160248: | Hours 24-25: Tychonoff and a taste of Stone-Cech (15). |
| 101111-160241: | Hours 24-25: Tychonoff and a taste of Stone-Cech (14). |
| 101111-155348: | Hours 24-25: Tychonoff and a taste of Stone-Cech (13). |
| 101111-154757: | Hours 24-25: Tychonoff and a taste of Stone-Cech (12). |
| 101111-154750: | Hours 24-25: Tychonoff and a taste of Stone-Cech (11). |
| 101111-154742: | Hours 24-25: Tychonoff and a taste of Stone-Cech (10). |
| 101111-152804: | Hours 24-25: Tychonoff and a taste of Stone-Cech (9). |
| 101111-152757: | Hours 24-25: Tychonoff and a taste of Stone-Cech (8). |
| 101111-152752: | Hours 24-25: Tychonoff and a taste of Stone-Cech (7). |
| 101111-145526: | Hours 24-25: Tychonoff and a taste of Stone-Cech (6). |
| 101111-145518: | Hours 24-25: Tychonoff and a taste of Stone-Cech (5). |
| 101111-145512: | Hours 24-25: Tychonoff and a taste of Stone-Cech (4). |
| 101111-143201: | Hours 24-25: Tychonoff and a taste of Stone-Cech (3). |
| 101111-143155: | Hours 24-25: Tychonoff and a taste of Stone-Cech (2). |
| 101111-143150: | Hours 24-25: Tychonoff and a taste of Stone-Cech. |
| 101104-155757: | Hours 22-23: Compactness in products and in metric spaces (18). |
| 101104-155746: | Hours 22-23: Compactness in products and in metric spaces (17). |
| 101104-155738: | Hours 22-23: Compactness in products and in metric spaces (16). |
| 101104-154358: | Hours 22-23: Compactness in products and in metric spaces (15). |
| 101104-154352: | Hours 22-23: Compactness in products and in metric spaces (14). |
| 101104-154347: | Hours 22-23: Compactness in products and in metric spaces (13). |
| 101104-153321: | Hours 22-23: Compactness in products and in metric spaces (12). |
| 101104-153315: | Hours 22-23: Compactness in products and in metric spaces (11). |
| 101104-153310: | Hours 22-23: Compactness in products and in metric spaces (10). |
| 101104-150945: | Hours 22-23: Compactness in products and in metric spaces (9). |
| 101104-150937: | Hours 22-23: Compactness in products and in metric spaces (8). |
| 101104-150927: | Hours 22-23: Compactness in products and in metric spaces (7). |
| 101104-144119: | Hours 22-23: Compactness in products and in metric spaces (6). |
| 101104-144114: | Hours 22-23: Compactness in products and in metric spaces (5). |
| 101104-144107: | Hours 22-23: Compactness in products and in metric spaces (4). |
| 101104-142355: | Hours 22-23: Compactness in products and in metric spaces (3). |
| 101104-142348: | Hours 22-23: Compactness in products and in metric spaces (2). |
| 101104-142342: | Hours 22-23: Compactness in products and in metric spaces. |
| 101101-145431: | Hour 21: Compact is closed and bounded, max values (8). |
| 101101-145425: | Hour 21: Compact is closed and bounded, max values (7). |
| 101101-145420: | Hour 21: Compact is closed and bounded, max values (6). |
| 101101-144322: | Hour 21: Compact is closed and bounded, max values (5). |
| 101101-144316: | Hour 21: Compact is closed and bounded, max values (4). |
| 101101-142729: | Hour 21: Compact is closed and bounded, max values (3). |
| 101101-142722: | Hour 21: Compact is closed and bounded, max values (2). |
| 101101-142717: | Hour 21: Compact is closed and bounded, max values. |
| 101025-145931: | Hour 18: Compactness of [0,1] (10). |
| 101025-145412: | Hour 18: Compactness of [0,1] (9). |
| 101025-145407: | Hour 18: Compactness of [0,1] (8). |
| 101025-145402: | Hour 18: Compactness of [0,1] (7). |
| 101025-143522: | Hour 18: Compactness of [0,1] (6). |
| 101025-143517: | Hour 18: Compactness of [0,1] (5). |
| 101025-143512: | Hour 18: Compactness of [0,1] (4). |
| 101025-142144: | Hour 18: Compactness of [0,1] (3). |
| 101025-142138: | Hour 18: Compactness of [0,1] (2). |
| 101025-142133: | Hour 18: Compactness of [0,1]. |
| 101021-160212: | Hours 16-17: Connectedness, path-connectedness, products (17). |
| 101021-160201: | Hours 16-17: Connectedness, path-connectedness, products (16). |
| 101021-155331: | Hours 16-17: Connectedness, path-connectedness, products (15). |
| 101021-155326: | Hours 16-17: Connectedness, path-connectedness, products (14). |
| 101021-155320: | Hours 16-17: Connectedness, path-connectedness, products (13). |
| 101021-153758: | Hours 16-17: Connectedness, path-connectedness, products (12). |
| 101021-153752: | Hours 16-17: Connectedness, path-connectedness, products (11). |
| 101021-153746: | Hours 16-17: Connectedness, path-connectedness, products (10). |
| 101021-151532: | Hours 16-17: Connectedness, path-connectedness, products (9). |
| 101021-151527: | Hours 16-17: Connectedness, path-connectedness, products (8). |
| 101021-151521: | Hours 16-17: Connectedness, path-connectedness, products (7). |
| 101021-144636: | Hours 16-17: Connectedness, path-connectedness, products (6). |
| 101021-144631: | Hours 16-17: Connectedness, path-connectedness, products (5). |
| 101021-144624: | Hours 16-17: Connectedness, path-connectedness, products (4). |
| 101021-143336: | Hours 16-17: Connectedness, path-connectedness, products (3). |
| 101021-143331: | Hours 16-17: Connectedness, path-connectedness, products (2). |
| 101021-143325: | Hours 16-17: Connectedness, path-connectedness, products. |
| 101018-150814: | Hour 15: Connectedness in R (11). |
| 101018-150802: | Hour 15: Connectedness in R (10). |
| 101018-145237: | Hour 15: Connectedness in R (9). |
| 101018-145231: | Hour 15: Connectedness in R (8). |
| 101018-145226: | Hour 15: Connectedness in R (7). |
| 101018-143926: | Hour 15: Connectedness in R (6). |
| 101018-143921: | Hour 15: Connectedness in R (5). |
| 101018-143914: | Hour 15: Connectedness in R (4). |
| 101018-141842: | Hour 15: Connectedness in R (3). |
| 101018-141836: | Hour 15: Connectedness in R (2). |
| 101018-141830: | Hour 15: Connectedness in R. |
| 101014-161227: | Hours 13-14: Metric spaces, sequencial closures, various products (16). |
| 101014-160029: | Hours 13-14: Metric spaces, sequencial closures, various products (15). |
| 101014-155102: | Hours 13-14: Metric spaces, sequencial closures, various products (14). |
| 101014-155057: | Hours 13-14: Metric spaces, sequencial closures, various products (13). |
| 101014-152903: | Hours 13-14: Metric spaces, sequencial closures, various products (12). |
| 101014-152858: | Hours 13-14: Metric spaces, sequencial closures, various products (11). |
| 101014-152852: | Hours 13-14: Metric spaces, sequencial closures, various products (10). |
| 101014-145913: | Hours 13-14: Metric spaces, sequencial closures, various products (9). |
| 101014-145907: | Hours 13-14: Metric spaces, sequencial closures, various products (8). |
| 101014-145900: | Hours 13-14: Metric spaces, sequencial closures, various products (7). |
| 101014-144558: | Hours 13-14: Metric spaces, sequencial closures, various products (6). |
| 101014-144553: | Hours 13-14: Metric spaces, sequencial closures, various products (5). |
| 101014-144548: | Hours 13-14: Metric spaces, sequencial closures, various products (4). |
| 101014-142719: | Hours 13-14: Metric spaces, sequencial closures, various products (3). |
| 101014-142713: | Hours 13-14: Metric spaces, sequencial closures, various products (2). |
| 101014-142707: | Hours 13-14: Metric spaces, sequencial closures, various products. |
| 101007-160238: | Hours 11-12: The box and the product topologies, metric spaces (15). |
| 101007-160232: | Hours 11-12: The box and the product topologies, metric spaces (14). |
| 101007-160224: | Hours 11-12: The box and the product topologies, metric spaces (13). |
| 101007-154817: | Hours 11-12: The box and the product topologies, metric spaces (12). |
| 101007-154811: | Hours 11-12: The box and the product topologies, metric spaces (11). |
| 101007-154804: | Hours 11-12: The box and the product topologies, metric spaces (10). |
| 101007-152848: | Hours 11-12: The box and the product topologies, metric spaces (9). |
| 101007-152842: | Hours 11-12: The box and the product topologies, metric spaces (8). |
| 101007-152836: | Hours 11-12: The box and the product topologies, metric spaces (7). |
| 101007-145418: | Hours 11-12: The box and the product topologies, metric spaces (6). |
| 101007-145412: | Hours 11-12: The box and the product topologies, metric spaces (5). |
| 101007-145406: | Hours 11-12: The box and the product topologies, metric spaces (4). |
| 101007-143300: | Hours 11-12: The box and the product topologies, metric spaces (3). |
| 101007-143255: | Hours 11-12: The box and the product topologies, metric spaces (2). |
| 101007-143249: | Hours 11-12: The box and the product topologies, metric spaces. |
| 101004-150154: | Hour 10: The axiom of choice and infinite product spaces (6). |
| 101004-145302: | Hour 10: The axiom of choice and infinite product spaces (5). |
| 101004-145256: | Hour 10: The axiom of choice and infinite product spaces (4). |
| 101004-143150: | Hour 10: The axiom of choice and infinite product spaces (3). |
| 101004-143144: | Hour 10: The axiom of choice and infinite product spaces (2). |
| 101004-143138: | Hour 10: The axiom of choice and infinite product spaces. |
| 100930-160134: | Hours 8-9: Separation axioms (12). |
| 100930-155431: | Hours 8-9: Separation axioms (11). |
| 100930-155417: | Hours 8-9: Separation axioms (10). |
| 100930-154237: | Hours 8-9: Separation axioms (9). |
| 100930-154229: | Hours 8-9: Separation axioms (8). |
| 100930-153416: | Hours 8-9: Separation axioms (7). |
| 100930-153407: | Hours 8-9: Separation axioms (6). |
| 100930-145752: | Hours 8-9: Separation axioms (5). |
| 100930-145746: | Hours 8-9: Separation axioms (4). |
| 100930-143647: | Hours 8-9: Separation axioms (3). |
| 100930-143631: | Hours 8-9: Separation axioms (2). |
| 100930-143624: | Hours 8-9: Separation axioms. |
| 100927-150035: | Hour 7: The Cantor Set, Closures (9). |
| 100927-150030: | Hour 7: The Cantor Set, Closures (8). |
| 100927-150024: | Hour 7: The Cantor Set, Closures (7). |
| 100927-144059: | Hour 7: The Cantor Set, Closures (6). |
| 100927-144052: | Hour 7: The Cantor Set, Closures (5). |
| 100927-144046: | Hour 7: The Cantor Set, Closures (4). |
| 100927-142710: | Hour 7: The Cantor Set, Closures (3). |
| 100927-142704: | Hour 7: The Cantor Set, Closures (2). |
| 100927-142655: | Hour 7: The Cantor Set, Closures. |
| 100923-155827: | Hours 5-6: Products, Subspaces, Closed Sets (14). |
| 100923-155821: | Hours 5-6: Products, Subspaces, Closed Sets (13). |
| 100923-155812: | Hours 5-6: Products, Subspaces, Closed Sets (12). |
| 100923-154754: | Hours 5-6: Products, Subspaces, Closed Sets (11). |
| 100923-154747: | Hours 5-6: Products, Subspaces, Closed Sets (10). |
| 100923-153713: | Hours 5-6: Products, Subspaces, Closed Sets (9). |
| 100923-152224: | Hours 5-6: Products, Subspaces, Closed Sets (8). |
| 100923-152216: | Hours 5-6: Products, Subspaces, Closed Sets (7). |
| 100923-150741: | Hours 5-6: Products, Subspaces, Closed Sets (6). |
| 100923-145401: | Hours 5-6: Products, Subspaces, Closed Sets (5). |
| 100923-145356: | Hours 5-6: Products, Subspaces, Closed Sets (4). |
| 100923-143415: | Hours 5-6: Products, Subspaces, Closed Sets (3). |
| 100923-143405: | Hours 5-6: Products, Subspaces, Closed Sets (2). |
| 100923-143358: | Hours 5-6: Products, Subspaces, Closed Sets. |
| 100920-145838: | Hour 4: Bases (9). |
| 100920-145831: | Hour 4: Bases (8). |
| 100920-145823: | Hour 4: Bases (7). |
| 100920-144614: | Hour 4: Bases (6). |
| 100920-144603: | Hour 4: Bases (5). |
| 100920-142955: | Hour 4: Bases (4). |
| 100920-142946: | Hour 4: Bases (3). |
| 100920-142938: | Hour 4: Bases (2). |
| 100920-141211: | Hour 4: Bases. |
| 100916-155901: | Hours 2-3: topologies, continuity, bases (15). |
| 100916-155414: | Hours 2-3: topologies, continuity, bases (14). |
| 100916-155406: | Hours 2-3: topologies, continuity, bases (13). |
| 100916-155401: | Hours 2-3: topologies, continuity, bases (12). |
| 100916-153251: | Hours 2-3: topologies, continuity, bases (11). |
| 100916-153246: | Hours 2-3: topologies, continuity, bases (10). |
| 100916-153240: | Hours 2-3: topologies, continuity, bases (9). |
| 100916-151018: | Hours 2-3: topologies, continuity, bases (8). |
| 100916-151007: | Hours 2-3: topologies, continuity, bases (7). |
| 100916-145130: | Hours 2-3: topologies, continuity, bases (6). |
| 100916-145122: | Hours 2-3: topologies, continuity, bases (5). |
| 100916-145117: | Hours 2-3: topologies, continuity, bases (4). |
| 100916-143834: | Hours 2-3: topologies, continuity, bases (3). |
| 100916-143824: | Hours 2-3: topologies, continuity, bases (2). |
| 100916-143818: | Hours 2-3: topologies, continuity, bases. |
| 100913-145848: | Hour 1: Continuity and open sets (5). |
| 100913-144833: | Hour 1: Continuity and open sets (4). |
| 100913-143313: | Hour 1: Continuity and open sets (3). |
| 100913-143305: | Hour 1: Continuity and open sets (2). |
| 100913-143258: | Hour 1: Continuity and open sets. |
| } |
Notes for BBS/10_327-101101-142717.jpg: [edit]