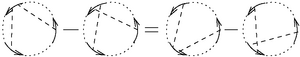VasCalc Documentation - User's Guide: Difference between revisions
No edit summary |
No edit summary |
||
| Line 194: | Line 194: | ||
First, let's make sure we get the same answer as the previous section with this presentation of the unknot: |
First, let's make sure we get the same answer as the previous section with this presentation of the unknot: |
||
[[Image:Unknot.jpg|thumb|60px|left|The unknot]] |
[[Image:Unknot.jpg|thumb|60px|left|The unknot]] |
||
{{In|n=14|in=<nowiki>unknot = MorseLink[Cup[1, 2], Cup[3, 4], X[2, |
{{In|n=14|in=<nowiki>unknot = MorseLink[Cup[1, 2], Cup[3, 4], X[2, Over, Up, Down], |
||
X[2, |
X[2,Under, Down, Up],Cap[2, 3], Cap[2, 1]];</nowiki>}} |
||
We'll compute the Kontsevich integral, reduce it, and print it out: |
We'll compute the Kontsevich integral, reduce it, and print it out: |
||
{{InOut|n=15|in=<nowiki>KontsevichIntegral[R, Phi, unknot] // ReduceFI // CD </nowiki> |
{{InOut|n=15|in=<nowiki>KontsevichIntegral[R, Phi, unknot] // ReduceFI // CD </nowiki> |
||
Revision as of 15:30, 9 September 2006
This page documents the ChordsMod4T component of the VasCalc project. This page is also under construction.
Overview
This package provides a Mathematica interface to work with the space generated by chord diagrams on a fixed skeleton of lines and circles, modulo the 4-T relation. See Dror Bar-Natan's Survey of Finite Type Invariants for further details.
Requirements
The software requirements of this package are Mathematica 4.1 and Java 1.4 (or greater, in both cases). However, note that default installations of Mathematica 4.1 and up include a Java runtime binary, and require no further configuration for this package to work.
In order to use the KontsevichIntegral, you must also install the KnotTheory` package, which is available from The Knot Atlas.
While there are no specific hardware requirements, the computations involved are rather resource-intensive. Users of low-end machines will see a smaller range of parameters for which the computation is practicable. We'll have an expected performance profile once work on this package is done.
Installation
If you have an up-to-date copy of the repository, skip ahead. If not, download ChordsMod4T.tar.gz and extract it to a directory of your choice.
You must also ensure that there is a directory named "CM4TData" under the installation directory, creating it if neccessary. This is for save/load functionality to work properly.
Usage
Initialization
If you wish to compute the KontsevichIntegral (and really, why else would you be here?), start by loading in the KnotTheory` package in a Mathematica session:
In[0]:=
|
<<KnotTheory`
|
Out[0]=
|
Loading KnotTheory` version of May 31, 2006, 14:15:20.091.
Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.
|
Also, load in the VasCalc definitions:
In[1]:=
|
<</path_to_install_folder/CDinterface.m
|
where "path_to_install_folder" is either the "trunk" folder of the repository, or the folder in which the above archive, if downloaded, was unpacked.
You must also issue the following command, to inform Mathematica of the location of the required Java objects:
In[2]:=
|
SetVasCalcPath["/path_to_install_folder"];
|
These steps must be followed at the start of each Mathematica session you wish to use this package.
Representing Chord Diagrams
Our convention for representing a chord diagram in Mathematica is through a CD object containing Line and Circle expressions as per the skeleton. To construct such a representation,
- Number the chords on the diagram.
- For each line on the skeleton, put within the brackets of its
Lineexpression the numbers of the chords that have their endpoints on that line, starting from the bottom and working up. For each circle, do the same, but one can choose an arbitrary starting point and count around. If there are no chords on a given line or circle, leave the brackets empty, as inLine[].
Naturally, there are many representations for a given diagram.
This package also allows for formal linear combinations of CD objects.
Computing chord diagram spaces modulo 4T and FI relations
The object CDSpace[l,m,n] represents the rational vector space generated by chord diagrams with n chords on a skeleton with l lines and m circles, modulo the 4-T relation. The first time a space is encountered in a session, a check is made to see if there is data for the required space on disc (under the path_to_install_folder/CM4TData directory). If no such entry exists, the space is computed, and by default the results are saved on disc for future use - this computation may be substantial, depending on the values of the parameters. One can prevent the saving of data by using the command CDSpace[l,m,n, WriteToDisc -> False] .
One can obtain the dimension of a chord diagram space, as follows:
In[3]:=
|
GetDimension[CDSpace[1,1,3]]
|
Out[3]=
|
19
|
One can also obtain a basis for a chord diagram space (modulo 4T), expressed as a list of chord diagrams:
In[4]:=
|
GetCDBasis[ CDSpace[1,1,3] ]
|
Out[4]=
|
{CD[Line[1, 1], Circle[2, 2, 3, 3]], CD[Line[1, 1], Circle[2, 3, 2, 3]],
CD[Line[1], Circle[1, 2, 3, 2, 3]], CD[Line[1], Circle[1, 2, 3, 3, 2]],
CD[Line[], Circle[1, 1, 2, 3, 3, 2]], CD[Line[1, 2, 1, 2], Circle[3, 3]],
CD[Line[], Circle[1, 2, 1, 3, 2, 3]], CD[Line[1, 2], Circle[1, 3, 3, 2]],
CD[Line[1, 2, 2, 1], Circle[3, 3]], CD[Line[1, 2, 2], Circle[1, 3, 3]],
CD[Line[], Circle[1, 2, 3, 1, 2, 3]], CD[Line[1, 2, 3], Circle[1, 3, 2]],
CD[Line[1, 2, 3, 2, 1, 3], Circle[]], CD[Line[1, 2, 3, 2], Circle[1, 3]],
CD[Line[1, 2, 3, 3], Circle[1, 2]], CD[Line[1, 2, 3, 2, 3, 1], Circle[]],
CD[Line[1, 2, 3, 2, 3], Circle[1]], CD[Line[1, 2, 3, 3, 2, 1], Circle[]],
CD[Line[1, 2, 3, 3, 2], Circle[1]]}
|
In addition, one can work with chord diagram spaces modulo the 4T and framing independence (FI) relations, using the command CDrSpace[l,m,n,opts] - the "r" stands for "further reduced". The above commands work in a similar fashion for these spaces.
Using ASeries objects
Because operations on chord diagrams (such as multiplication and reduction) can often be resource-intensive, it is desirable to work with representations in Java as much as possible. The ASeries object is meant to facilitate this. To create one, use the command ASeries[Permutation, m, CDcombo], where
Permutationis a list of integers from 1 tol(the number of strands) which encode the permutation of those strands that theASeriesis intended to represent (Note -Id[n]can be used as a shortcut for the identity permutation onnstrands). For example, if one wishes a combination of chord diagrams to represent the braiding of the first two strands in a skeleton of five strands, one would use the permutation{2,1,3,4,5},mis the number of circles, andCDcombois a linear combination of chord diagrams (represented byCD's, and possibly a constant term), all of which are on a fixed skeleton ofllines andmcircles, and may have a different number of chords.
It is important to note that an ASeries carries with it the notion of an order, defined implicitly by the maximum number of chords to appear in a diagram in CDcombo; the result of any and all computations are only given up to the lowest order appearing therein. To force a maximum order, use the command ASeries[Permutation, m, CDCombo, MaxDegree], where MaxDegree is a non-negative integer.
There are several operations one can perform on an ASeries object. Addition and multiplication is achieved using the + and . operators respectively - however only diagrams representing the same permutation can be added. Multiplication naturally composes the permutations. Also, ASeries objects can be inverted (up to the highest order), provided they are of the form (1 + higher order terms) .
Additionally, the following unary operations are available:
AddStrand[n, ASeries]adds an empty strand to all the diagrams in the givenASeriesafter then'th position.DoubleStrand[n, ASeries]doubles then'th strand in all the diagrams in the givenASeries.ReverseStrand[n, ASeries]reverses then'th strand in all the diagrams in the givenASeries.ConnectStrand[i, j, ASeries]is the linear extension of the operation that for each diagram, appends thej'th strand to the end of thei'th one.Reduce[ASeries]returns anotherASeriesequivalent to the first modulo the 4T relation. This operation may take some time if the relevant chord diagram spaces need to be computed.ReduceFI[ASeries]returns anotherASeriesequivalent to the first modulo the 4T relation, and the FI relations. As before, this operation may take some time if the relevant chord diagram spaces need to be computed.
All these operations will be put to use in the next section.
Finally, to convert an ASeries back to a human-readable form, use the command: CD[ AS ], where AS is the object to be converted.
Checking the pentagon and hexagon relations
For paranthesized braids, the pentagon and hexagon equations are given by
|

|
| The Pentagon and the Hexagons for Parenthesized Braids | |
.
Algebraically, these relations can be written as
| [Pentagon] |
| [Hexagons] |
where is the algebra of chord diagrams on strands modulo the 4-T relations.
Let us check that a proposed pair satisfy these equations, up to the third order. After running through the initialization above, we introduce our candidates as ASeries objects - note that we wish to represent a transposition, while is a trivial permutation:
In[3]:=
|
Phi = ASeries[{1, 2, 3}, 0,
1 + (1/24)*CD[Line[1], Line[2], Line[1, 2]] -
(1/24)*CD[Line[2], Line[1], Line[1, 2]], 3]
]
|
Out[3]=
|
ASeries[{1, 2, 3}, 0, {«JavaObject[vectorSpace.Coefficient]»,
«JavaObject[vectorSpace.Coefficient]», «JavaObject[ChordVector]»,
«JavaObject[vectorSpace.Coefficient]»}]
|
In[4]:=
|
R = ASeries[{2, 1}, 0,
1 + (1/2)CD[Line[1], Line[1]] + (1/8)CD[Line[1, 2],Line[1, 2]] +
(1/48)CD[Line[1, 2, 3], Line[1, 2, 3]]
]
|
Out[4]=
|
ASeries[{2, 1}, 0, {«JavaObject[vectorSpace.Coefficient]»,
«JavaObject[ChordVector]», «JavaObject[ChordVector]»,
«JavaObject[ChordVector]»}]
|
First, we'll check the pentagon equation. Writing the difference of the two sides for ,
In[5]:=
|
AddStrand[0, Phi].DoubleStrand[2, Phi].AddStrand[3, Phi] -
DoubleStrand[1, Phi].DoubleStrand[3, Phi]
|
Out[5]=
|
ASeries[{1,2,3,4}, 0, {«JavaObject[vectorSpace.Coefficient]»,
«JavaObject[ChordVector]», «JavaObject[ChordVector]»}]
|
Now we reduce the result modulo the 4T relations, and convert back to CD notation:
In[6]:=
|
CD[Reduce[%]]
|
Out[6]=
|
0
|
Thus our candidate solves the pentagon equation.
Let's also test one of the hexagon equations:
In[7]:=
|
DoubleStrand[1, R] - Phi.AddStrand[0, R].(Phi)^(-1).AddStrand[2, R].Phi
|
Out[7]=
|
ASeries[{2,3,1}, 0, {«JavaObject[vectorSpace.Coefficient]»,
«JavaObject[ChordVector]», «JavaObject[ChordVector]»}]
|
Reducing the result, we see that our choices of and yield a solution to the first hexagon equation.
In[8]:=
|
CD[Reduce[%]]
|
Out[8]=
|
0
|
The second hexagon equation can be verified in a similar fashion, and the result is the same.
Braid Invariants
To come: definition of Z[B[n]], demonstration of Reidemeister moves. For now, reidemeister.nb.
The Unknot
To compute for any knot, including the unknot, we need to extend the definition of to include "caps" and "cups". In addition, framing independence forces us to introduce the FI relation - hence all the formulae in this section take place in the "further reduced" space of chord diagrams. We proceed using the correction term in [1]. To begin, let us choose a pair which solve the pentagon and hexagon equations to fourth degree:
In[9]:=
|
Phi = ASeries[Id[3],0,
1 + CD[Line[1], Line[2], Line[1, 2]]/24 -
(7*CD[Line[1], Line[2, 3, 4], Line[1, 2, 3, 4]])/5760 -
CD[Line[2], Line[1], Line[1, 2]]/24 +
(7*CD[Line[2], Line[1, 3, 4], Line[1, 2, 3, 4]])/1920 -
(7*CD[Line[3], Line[1, 2, 4], Line[1, 2, 3, 4]])/1920 +
(7*CD[Line[4], Line[1, 2, 3], Line[1, 2, 3, 4]])/5760 +
(7*CD[Line[1, 2], Line[3, 4], Line[1, 2, 3, 4]])/5760 -
CD[Line[1, 3], Line[2, 4], Line[1, 2, 3, 4]]/640 -
CD[Line[1, 4], Line[2, 3], Line[1, 2, 3, 4]]/1152 -
CD[Line[2, 3], Line[1, 4], Line[1, 2, 3, 4]]/1152 +
(19*CD[Line[2, 4], Line[1, 3], Line[1, 2, 3, 4]])/5760 -
(7*CD[Line[3, 4], Line[1, 2], Line[1, 2, 3, 4]])/5760 -
CD[Line[1, 2, 3], Line[4], Line[1, 2, 3, 4]]/1440 +
CD[Line[1, 2, 4], Line[3], Line[1, 2, 3, 4]]/480 -
CD[Line[1, 3, 4], Line[2], Line[1, 2, 3, 4]]/480 +
CD[Line[2, 3, 4], Line[1], Line[1, 2, 3, 4]]/1440
];
|
In[10]:=
|
R = ASeries[{2,1},0,
1 + CD[Line[1], Line[1]]/2 + CD[Line[1, 2], Line[1, 2]]/8 +
CD[Line[1, 2, 3], Line[1, 2, 3]]/48 +
CD[Line[1, 2, 3, 4], Line[1, 2, 3, 4]]/384
];
|
The definition of involves going up the third strand, down the second, and up the first strand of :
In[11]:=
|
Zinf = ConnectStrand[2,1, ConnectStrand[3,2, ReverseStrand[2,Phi] ] ]
|
Out[11]=
|
ASeries[{1}, 0, {«JavaObject[vectorSpace.Coefficient]»,
«JavaObject[vectorSpace.Coefficient]», «JavaObject[ChordVector]»,
«JavaObject[vectorSpace.Coefficient]», «JavaObject[ChordVector]»}]
|
The invariant of the unknot is given by closing to a circle (the first line below), and taking the inverse:
In[12]:=
|
ZinfInverseCircle = ASeries[0,1,CD[(Zinf)^(-1)] /. Line -> Circle]
|
Out[12]=
|
ASeries[0, 1, {«JavaObject[vectorSpace.Coefficient]»,
«JavaObject[vectorSpace.Coefficient]», «JavaObject[ChordVector]»,
«JavaObject[vectorSpace.Coefficient]», «JavaObject[ChordVector]»}]
|
In[13]:=
|
CD[ReduceFI[ZinfInverseCircle]]
|
Out[13]=
|
1 - CD[Circle[1, 2, 1, 2]]/24 - CD[Circle[1, 2, 3, 1, 4, 2, 3, 4]]/360 +
CD[Circle[1, 2, 3, 1, 4, 3, 2, 4]]/720 + (7*CD[Circle[1, 2, 3, 4, 1, 2, 3, 4]])/5760
|
The Kontsevich integral for unframed knots
We can find the Kontsevich integral of any knot K, through the command KontsevichIntegral[R, Phi, K], where R and Phi are ASeries objects as above, and K is a Morse link presentation of a knot (or alternatively any presentation that KnotTheory` knows how to convert to a Morse link presentation). The output, for a knot, is an ASeries object on one circle, whose degree is determined by the degrees of R and Phi.
In these examples, we shall continue to use the pair defined in the previous section.
First, let's make sure we get the same answer as the previous section with this presentation of the unknot:
In[14]:=
|
unknot = MorseLink[Cup[1, 2], Cup[3, 4], X[2, Over, Up, Down],
X[2,Under, Down, Up],Cap[2, 3], Cap[2, 1]];
|
We'll compute the Kontsevich integral, reduce it, and print it out:
In[15]:=
|
KontsevichIntegral[R, Phi, unknot] // ReduceFI // CD
|
Out[15]=
|
1 - CD[Circle[1, 2, 1, 2]]/24 - CD[Circle[1, 2, 3, 1, 4, 2, 3, 4]]/360 +
CD[Circle[1, 2, 3, 1, 4, 3, 2, 4]]/720 + (7*CD[Circle[1, 2, 3, 4, 1, 2, 3, 4]])/5760
|
Performance Issues
We are currently working to improve the performance of this program. For larger computations, it would likely help to increase the maximum heap size available to Java. To do this, type the following into Mathematica before loading the CDinterface.m definitions (step 1 above):
In[1]:=
|
Needs["JLink`"];
|
In[2]:=
|
InstallJava[CommandLine -> "/path_to_java_runtime/java -Xmx128M"]
|
This allows Java to use up to 128 megabytes of memory; you may change the number "128" in the parameter "-Xmx128M" to suit your needs. Note that the first line needs to be entered exactly as shown - the funny apostrophe is located next to the "1" key on many keyboards.
References
- [1] D. Bar-Natan, Non-Associative Tangles. Geometric Topology (proceedings of the Georgia International Topology Conference, W. H. Kazez ed.), 139-183, Amer. Math. Soc. and International Press, Providence, 1997.