VS, TS and TG Algebras
|
Abstract
We introduce VS-, TS- and TG-Algebras; three types of algebraic entities within which some basic equations of knot theory (related to Algebraic Knot Theory) can be written and potentially solved.
Why Bother?
- These equations are valuable yet not well understood. My hope is to study them in many simpler spaces (i.e., in many simpler VS-, TS- and TG-Algebras) than the ones that naturally occur in knot theory, in the hope that out of many test cases an understanding will emerge.
- In particular, one day I hope to write (or encourage the writing of) computer programs that will take a VS-, TS-, or TG-algebra "plug-in" and given it, will carry out all the necessary higher-level algebra. This will make it easier to study particular cases computationally. But for this, the notions of VS-, TS- and TG-Algebras must first be completely specified.
VS-Algebras in One Paragraph
A VS-Algebra (Vertical Strands Algebra) is an algebraic object that is endowed with the same operations as the algebras of horizontal chord chord diagrams - multiplication (vertical stacking, a binary operation) and strand permutation, strand addition, strand doubling and strand deletion (all unary operations). It is local if it satisfies the same "locality in time" and "locality in space" relations that satisfies [Bar-Natan_97]. In any local VS-algebra the equations for a Drinfel'd associator (i.e., the pentagon and the hexagon) can be written and potentially be solved, and solutions always lead to braid invariants. Likewise in any local VS-algebra the largely undocumented braidor equations can be written and potentially be solved, and solutions always lead to braid invariants.
TS-Algebras in One Paragraph
A TS-Algebra (Tangled Strands Algebra) is to tangles as a VS-algebra is to braids. Equally cryptically, it is to as a VS-algebra is to . Thus a TS-algebra has the same unary operations as a VS-algebra along with a fancier collection of "products" that allow for "reversing" and "bending back" strands before they are concatenated. Thus every TS-algebra is in particular a VS-algebra, hence if it is "local" (with the same definition as for a VS-algebra), associators and braidors make sense it it. In a TS-algebra every associator or braidor satisfying some minor further symmetry conditions leads to a knot and link invariant. Furthermore, sufficiently symmetric associators lead to full-fledged Algebraic Knot Theories.
TG-Algebras in One Paragraph
A TG-Algebra (Trivalent Graph Algebra) is to knotted trivalent graphs as a TS-algebra is to tangles. Knotted trivalent graphs are equivalent to tangles, in some topological sense; indeed, given a knotted trivalent graph, pick a maximal tree and contract it until it is just a thick point. What remains, in the complement of that think point, is just a number of knotted edges with no vertices. That is, it is a tangle. It follows that a knotted trivalent graph is merely a tangle with just a bit of extra combinatorial labeling. Likewise the notions of a TG-algebra and of a TS-algebra are nearly equivalent. They differ mostly just by how certain things are labeled.
VS-Algebras in Some Detail
The basic definitions
Definition. For a natural number let denote the set . Let denote the category whose objects are the natural numbers and whose morphisms are given by
with the obvious composition of morphisms. For brevity we will often specify morphisms/functions by simply listing their values, omitting the value at as it is anyway fixed. Thus for example, , or even shorter, , means with , , and (strictly speaking, the target space of can be any with ).
Interpretation. The object "" stands for " strands". A morphism means "for any , strand number in looks at strand number in if , and looks nowhere if ".
Definition. A VS-algebra is a contravariant functor from the category to the category of algebras over some fixed ring of scalars. We denote by and by .
Interpretation. In a TS-algebra we have an algebra for any number of strands, with multiplication corresponding to "stacking two -stranded objects (imagine braids) one on top the other". We think of an element of as " strands each of which carrying some algebraic information". If , then has strands carrying algebraic information, and if , strand number in "reads" its information from strand number in . If , strand number in reads its information from nowhere, so it carries some "default" information, presumably "empty".
You are probably familiar with the notation used elsewhere (in [Bar-Natan_97], for example) when dealing with associators and the pentagon and hexagon equations. Here's a quick dictionary:
| Elsewhere | In Words | Here | In Words |
| Copy the first strand untouched and double the second strand | The first output strand reads from the first input strand, the second and third both read from the second. | ||
| Delete the second strand. | Nothing reads from the second strand, as isn't in the range of . | ||
| Add an empty strand on the left. | The first strand reads from nowhere to it is empty. The second and third output strands read from the first and second input strands respectively. | ||
| Permute the strands: Install on , on and on . | Permute the strands: Read from , from and from . |
Thus the new notation is the opposite of the old when it comes to permutations: if is a permutation, is now . It is a small price to pay considering the very short description (as above) that now becomes available for VS-algebras.
The VS-Algebra of legs and VS-algebras of animals
One of the most fundamental VS-Algebras is the VS-algebra of "legs", defined as follows. Set to be the free associative and commutative algebra generated by "leg symbols" (think, " is a leg on strand number "). Then let
(thus strand number in the output looks at strand number in the input, and if it sees a leg there, it takes a copy). It is a routine exercise to verify that is indeed a VS-algebra.
An "animal" is a formal symbol with a fixed number of "legs", and it is bilinear in those legs. Thus for example we may declare that the animal has three legs, and so "a animal in " will be a symbol of the form where , and are legs in (thus ), and animals get pulled back as the sum of all ways of pulling back their legs:
| *The superscript "" stands for "non-local". A local version of this VS-algebra will be introduced after locality is introduced further below. |
Once we choose our formal symbols for animals, we may consider the free associative (though not commutative!) algebra generated by all such animals with legs in and the resulting collection of algebras and pullback operations will form a VS-algebra*.
The most standard example is the two-legged animal often referred to as "a chord from strand to strand "; this animal is also declared to be symmetric - it is declared that for all and . The resulting VS-algebra is the VS-algebra of (non-local) "horizontal chords".
The pentagon and the hexagons
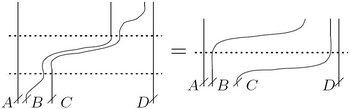
|

|
| The Pentagon and the Hexagons for Parenthesized Braids | |
The main thing I'd like to do in a VS-algebra is to write and solve the pentagon and hexagons equations. The unknowns in these equations are an invertible element and an invertible element , and the equations read:
| [Pentagon] |
and
| [Hexagons] |
In old notation, this is:
and
Locality
Definition. A VS-algebra is called "local" if in whenever " regards the strands that is supported on as equivalent". More precisely, whenever for , where and and where is constant on the subset of on which is non-zero.
It is an excellent idea to pause briefly and try to see why the informal part of the above definition matches with it formal part. Also, if you know about "locality in space" and "locality in scale" as they are described in [Bar-Natan_97], it is an excellent idea to verify that our single notion of locality is equivalent to the conjunction of the two localities of that paper. Finally, it is clear that every VS-algebra can be made local by imposing the relation whenever necessary. Thus the VS-algebras "of animals" above also have local versions. We leave it as an exercise to our readers to verify that the local version of the non-local VS-algebra of horizontal chords, defined above, is the well known algebra of horizontal chord diagrams modulo relations of the theory of finite type invariants of braids.
Theorem. Any solution of the pentagon and hexagon equations in a local VS-algebra leads to an invariant of braids.
Of course, this theorem is not quite well-formulated; strictly speaking one can always take the invariant of braids in the theorem to be the trivial invariant. So the theorem fully makes sense only after its proof is given. But we have no intention of providing a proof here - the theorem and its proof are quite obvious if you think in the spirit of [Bar-Natan_97].
Solutions in the graded case
If a local VS-algebra is graded in the obvious sense and if every has an identity element in degree 0 one can run exactly the same iterative degree-by-degree procedure as in [Bar-Natan_97] in attempt to find solutions to the pentagon and hexagon. The existence and uniqueness of such solutions is then goverened by exactly the same homology theory as in [Bar-Natan_97], with obvious adjustments made to accomodate for the more general setup. However, for different VS-algebras the corresponding homology groups may or may not be trivial and hence solutions may or may not exist. Thus comes our main question:
Question. Find examples of local VS-algebras to illuminate the various existence/uniqueness possibilities. Examples in which a pair exists and is unique, examples in which a solution isn't unique but the different solutions can be enumerated in a reasonable way, etc. Also, find examples of local VS-algebras in which solutions can be written in "closed form".
My paperlet Associators with Frozen Feet is about the simplest non-trivial local VS-algebra I am aware off in which closed-form solutions seem to exist. A similar example is implicitly in [Kurlin_04].
TS-Algebras in Some Detail
Enumerating r-ary operations and multicategories
In the previous section we've defined VS-algebras using contravariant functors on the category . For the purpose of our game, is "that thing which enumerates the spaces and operations in a VS-algebras"; a VS-algebra has one space for each object of (i.e., for each integer) and one operation for each morphism in . More precisely, does not enumerate all the operations in a VS-algebra - only the unary ones. As is the case for the set of braids, a VS-algebra has some, though very few, -ary operations as well, corresponding to "vertical stacking". These we have included into the structure by insisting that each space in a VS-algebra be an algebra, hence equipped with a binary operation. Higher -ary operations are simply iterated compositions of the binary product.
As said before, a TS-algebra is to tangles as a VS-algebra is to braids. But tangles can be composed in many more ways than braids and so in enumerating all the operations in a TS-algebra we will need a more sophisticated approach. No longer will it be enough to enumerate unary operations using a category and then to throw in a single binary operation almost as an afterthought. We now need to genuinely enumerate all -ary operations for all .
The formal tool for enumerating -ary operations is a certain cross of a category and an operad called a "multicategory". In short, a multicategory has objects and identity morphisms like in an ordinary category but its sets of morphisms (which really should be called "multimorphisms") depend on "input objects" and one "output object". Such morphisms can be composed much like ordinary -ary operations, and a certain associativity of the composition maps is required. In a multicategory , we will denote the set of multimorphisms whose input objects are and whose output object is by .
The Multicategory TS
Let be the multicategory whose objects are the natural numbers and whose morphism are
TG-Algebras is Some Detail
This section will surely wait a while to be written; at the moment I don't have an immediate reason to write it nor do I know exactly what I want written.
References
[Bar-Natan_97] ^ Dror Bar-Natan, Non-Associative Tangles, in Geometric topology, proceedings of the Georgia international topology conference, W. H. Kazez, ed., 139-183, Amer. Math. Soc. and International Press, Providence, 1997.
[Kurlin_04] ^ Vitaliy Kurlin, Compressed Drinfel'd Associators, arXiv:math.GT/0408398.































































































