User:Sankaran/06-1350-HW4: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
Warning - nothing new yet... |
|||
===The Generators=== |
===The Generators=== |
||
| Line 7: | Line 7: | ||
|- align=center valign=middle |
|- align=center valign=middle |
||
|align=left|Picture |
|align=left|Picture |
||
|[[Image:06-1350-T.svg|100px]] |
|||
| ⚫ | |||
|[[Image:06-1350-R.svg|100px]] |
|||
| ⚫ | |||
|[[Image:06-1350-Phi.svg|100px]] |
|||
| ⚫ | |||
|[[Image:06-1350-BPlus.svg|100px]] |
|[[Image:06-1350-BPlus.svg|100px]] |
||
|[[Image:06-1350-BMinus.svg|100px]] |
|||
| ⚫ | |||
|- align=center valign=middle |
|- align=center valign=middle |
||
|align=left|Generator |
|align=left|Generator |
||
| Line 28: | Line 28: | ||
|} |
|} |
||
(Thanks [[User:Zak/06-1350-HW4|Zavosh]] for the nice picture) |
|||
===The Relations=== |
===The Relations=== |
||
====The Reidemeister Move R2==== |
|||
(Courtesy of Andy) |
|||
[[Image:06-1350-R2-weird.png|center]] |
|||
In formulas, this is |
|||
<center><math>1 = (123)^\star B^- (132)^\star B^+.</math></center> |
|||
Linearized and written in functional form, this becomes |
|||
{| align=center |
|||
| ⚫ | |||
|<math>\rho_2(x_1,x_2,x_3) = - b^-(x_1,x_2,x_3) - b^+(x_1,x_3,x_2).</math> |
|||
| ⚫ | |||
====The Reidemeister Move R3==== |
====The Reidemeister Move R3==== |
||
(Picture and first example courtesy of Dror) |
|||
| ⚫ | |||
There are eight of these (each crossing in the picture can be + or - ). |
|||
| ⚫ | |||
[[Image:06-1350-R4.svg|400px|center]] |
[[Image:06-1350-R4.svg|400px|center]] |
||
In formulas, this is |
In formulas, this is |
||
| Line 38: | Line 54: | ||
{| align=center |
{| align=center |
||
|- |
|- |
||
|<math>\rho_3(x_1, x_2, x_3, x_4) = </math> |
|<math>\rho_3[+++](x_1, x_2, x_3, x_4) = </math> |
||
|<math>b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4)</math> |
|<math>b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4)</math> |
||
|- |
|- |
||
| Line 44: | Line 60: | ||
|<math>- b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3).</math> |
|<math>- b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3).</math> |
||
|} |
|} |
||
Here are the rest of them, linearized and in functional form - I think this is too many, but it's probably easier to write these out than to figure the relationships between them. Also, some better notation is needed. |
|||
<math>\rho_3[++-](x_1,x_2,x_3,x_4) = b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^-(x_1,x_3,x_4) |
|||
- b^-(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3).</math> |
|||
<math>\rho_3[+-+](x_1,x_2,x_3,x_4) = b^+(x_1,x_2,x_3) + b^-(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4)- b^+(x_1+x_2,x_3,x_4) - b^-(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3). </math> |
|||
<math>\rho_3[-++](x_1,x_2,x_3,x_4) = b^-(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4)- b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^-(x_1+x_4,x_2,x_3). </math> |
|||
<math>\rho_3[+--](x_1,x_2,x_3,x_4) = b^+(x_1,x_2,x_3) + b^-(x_1+x_3,x_2,x_4) + b^-(x_1,x_3,x_4)- b^-(x_1+x_2,x_3,x_4) - b^-(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3). </math> |
|||
<math>\rho_3[-+-](x_1,x_2,x_3,x_4) = b^-(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^-(x_1,x_3,x_4)- b^-(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^-(x_1+x_4,x_2,x_3). </math> |
|||
<math>\rho_3[--+](x_1,x_2,x_3,x_4) = b^-(x_1,x_2,x_3) + b^-(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4)- b^+(x_1+x_2,x_3,x_4) - b^-(x_1,x_2,x_4) - b^-(x_1+x_4,x_2,x_3). </math> |
|||
<math>\rho_3[---](x_1,x_2,x_3,x_4) = b^-(x_1,x_2,x_3) + b^-(x_1+x_3,x_2,x_4) + b^-(x_1,x_3,x_4)- b^-(x_1+x_2,x_3,x_4) - b^-(x_1,x_2,x_4) - b^-(x_1+x_4,x_2,x_3). </math> |
|||
====The Reidemeister Move R4==== |
|||
(Courtesy of Andy) |
|||
There are two (ostensibly) different versions: |
|||
[[Image:06-1350-R4a.png|center]] |
|||
In formulas, this is |
|||
<center><math>(1230)^\star B^+ (1213)^\star B^+ (1023)^\star \Phi = (1123)^\star \Phi (1233)^\star B^+</math>.</center> |
|||
Linearized and written in functional form, this becomes |
|||
{| align=center |
|||
| ⚫ | |||
|<math>\rho_{4a}(x_1,x_2,x_3,x_4) = b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + \phi(x_1,x_3,x_4) - \phi(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_3+x_4).</math> |
|||
| ⚫ | |||
Second: |
|||
[[Image:06-1350-R4b.png|center]] |
|||
In formulas, this is |
|||
<center><math>(1123)^\star B^+ (1203)^\star B^+ (1231)^\star \Phi = (1230)^\star \Phi (1223)^\star B^+</math>.</center> |
|||
Linearized and written in functional form, this becomes |
|||
{| align=center |
|||
|- |
|||
|<math>\rho_{4b}(x_1,x_2,x_3,x_4) = b^+(x_1+x_2,x_3,x_4) + b^+(x_1,x_2,x_4) + \phi(x_1+x_4,x_2,x_3) - \phi(x_1,x_2,x_3) - b^+(x_1,x_2+x_3,x_4).</math> |
|||
|} |
|||
===The Syzygies=== |
===The Syzygies=== |
||
Latest revision as of 18:04, 12 December 2006
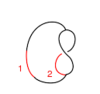
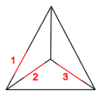
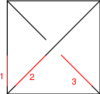
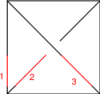
The Generators
Our generators are , , and :
| Picture | 
|
|
|
|
|
| Generator | |||||
| Perturbation |
(Thanks Zavosh for the nice picture)
The Relations
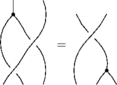
The Reidemeister Move R2
(Courtesy of Andy)
In formulas, this is
Linearized and written in functional form, this becomes
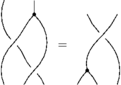
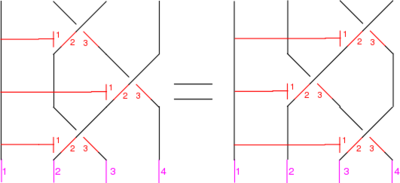
The Reidemeister Move R3
(Picture and first example courtesy of Dror)
There are eight of these (each crossing in the picture can be + or - ). For example, if all the crossings are positive, the picture (with three sides of the shielding removed) is
In formulas, this is
Linearized and written in functional form, this becomes
=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/231c9b6d709699bf392b563aa45d79f0417696b4)
Here are the rest of them, linearized and in functional form - I think this is too many, but it's probably easier to write these out than to figure the relationships between them. Also, some better notation is needed.
=b^{+}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{4})-b^{+}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06cd8b9b7e138b986be80a0e180a4946404b6c5d)
=b^{+}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{+}(x_{1},x_{3},x_{4})-b^{+}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{+}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e8055a80d8382baf7a0ff635102c605c27eda4b)
=b^{-}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+b^{+}(x_{1},x_{3},x_{4})-b^{+}(x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fce40ea9085985c87aecd8bb5c98ad52bce483ee)
=b^{+}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{+}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bff9ab040ba74e0c7cd17a0b5af34a4890080cc)
=b^{-}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/298ba6b42ae81403d32cd6a4b088b2957360bd25)
=b^{-}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{+}(x_{1},x_{3},x_{4})-b^{+}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e950790f43156dae93842d5adc65327387c192a5)
=b^{-}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/293afcc6fc1c13efd70b97455e6723a225863a56)
The Reidemeister Move R4
(Courtesy of Andy)
There are two (ostensibly) different versions:
In formulas, this is
Linearized and written in functional form, this becomes
Second:
In formulas, this is
Linearized and written in functional form, this becomes
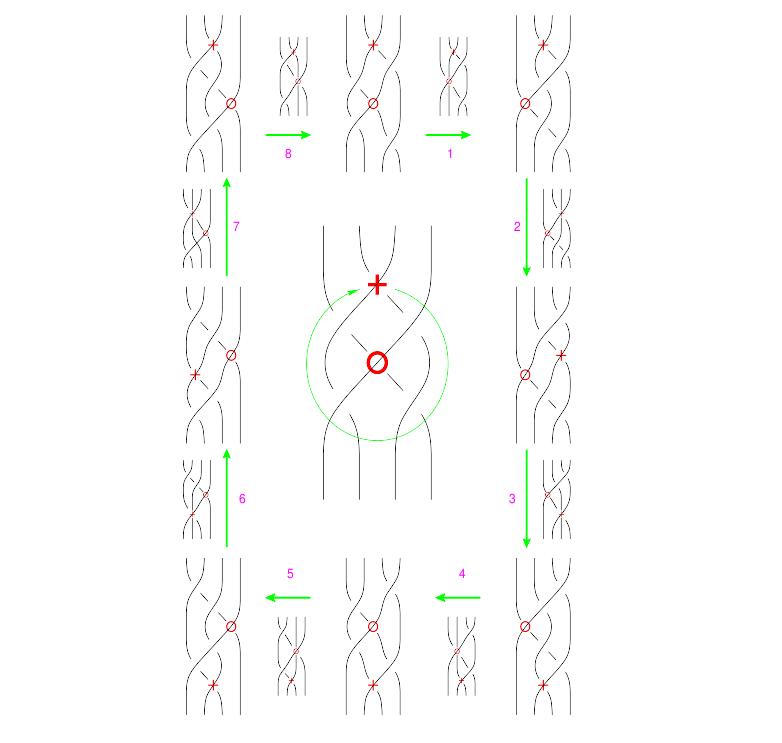
The Syzygies
The "B around B" Syzygy
The picture, with all shielding removed, is
 |
| (Drawn with Inkscape) (note that lower quality pictures are also acceptable) |
The functional form of this syzygy is
A Mathematica Verification
The following simulated Mathematica session proves that for our single relation and single syzygy, . Copy paste it into a live Mathematica session to see that it's right!
In[1]:=
|
d1 = {
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] +
bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] -
bp[x1 + x4, x2, x3]
};
d2 = {
BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] +
rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] -
rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] -
rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] +
rho3[x1 + x3, x2, x4, x5]
};
|
In[3]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2
|
Out[3]=
|
- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5]
+ rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5]
+ rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5]
+ rho3[x1 + x5, x2, x3, x4]
|
In[4]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
|
Out[4]=
|
0
|
