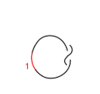
The Generators
Our generators are  ,
,  ,
,  and
and  :
:
| Picture
|
|
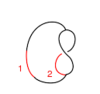
|
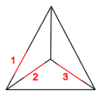
|
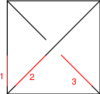
|
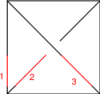
|
| Generator
|

|

|

|

|

|
| Perturbation
|

|

|

|

|

|
(Thanks Zavosh for the nice picture)
The Relations
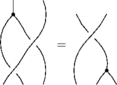
The Reidemeister Move R2
(Courtesy of Andy)
In formulas, this is

Linearized and written in functional form, this becomes

|
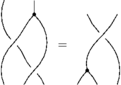
The Reidemeister Move R3
(Picture and first example courtesy of Dror)
There are eight of these (each crossing in the picture can be + or - ).
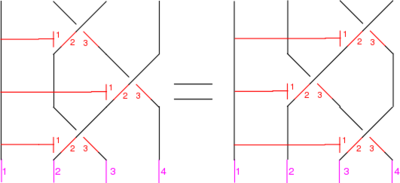
For example, if all the crossings are positive, the picture (with three sides of the shielding removed) is
In formulas, this is
 .
.
Linearized and written in functional form, this becomes
=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/231c9b6d709699bf392b563aa45d79f0417696b4)
|

|
|
|

|
Here are the rest of them, linearized and in functional form - I think this is too many, but it's probably easier to write these out than to figure the relationships between them. Also, some better notation is needed.
=b^{+}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{4})-b^{+}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06cd8b9b7e138b986be80a0e180a4946404b6c5d)
=b^{+}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{+}(x_{1},x_{3},x_{4})-b^{+}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{+}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e8055a80d8382baf7a0ff635102c605c27eda4b)
=b^{-}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+b^{+}(x_{1},x_{3},x_{4})-b^{+}(x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fce40ea9085985c87aecd8bb5c98ad52bce483ee)
=b^{+}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{+}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bff9ab040ba74e0c7cd17a0b5af34a4890080cc)
=b^{-}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/298ba6b42ae81403d32cd6a4b088b2957360bd25)
=b^{-}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{+}(x_{1},x_{3},x_{4})-b^{+}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e950790f43156dae93842d5adc65327387c192a5)
=b^{-}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/293afcc6fc1c13efd70b97455e6723a225863a56)
The Reidemeister Move R4
(Courtesy of Andy)
There are two (ostensibly) different versions:
In formulas, this is
 .
.
Linearized and written in functional form, this becomes

|
Second:
In formulas, this is
 .
.
Linearized and written in functional form, this becomes

|
The Syzygies
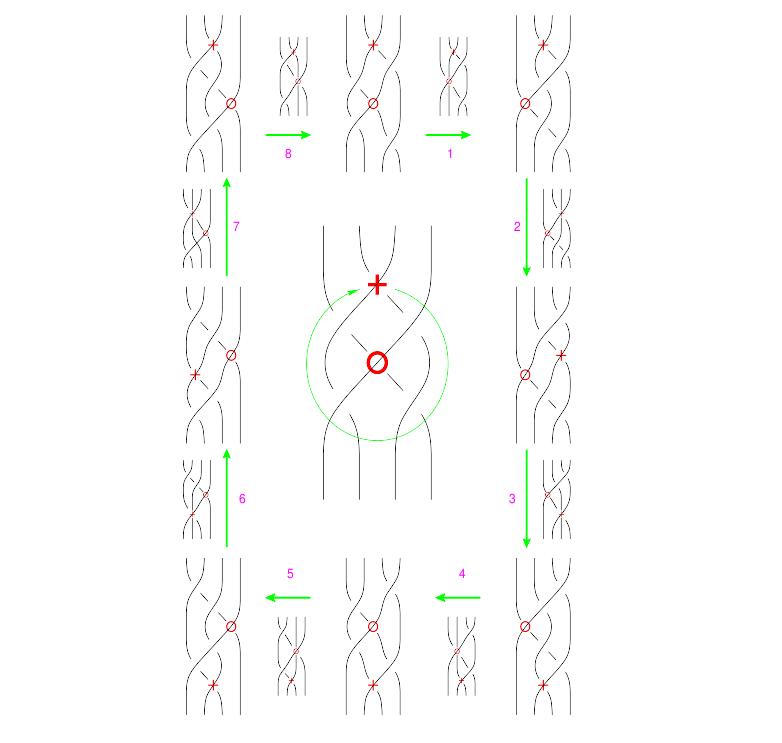
The "B around B" Syzygy
The picture, with all shielding removed, is
|
|
(Drawn with Inkscape)
(note that lower quality pictures are also acceptable)
|
The functional form of this syzygy is

|

|
|
|

|
|
|

|
A Mathematica Verification
The following simulated Mathematica session proves that for our single relation and single syzygy,  . Copy paste it into a live Mathematica session to see that it's right!
. Copy paste it into a live Mathematica session to see that it's right!
In[1]:=
|
d1 = {
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] +
bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] -
bp[x1 + x4, x2, x3]
};
d2 = {
BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] +
rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] -
rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] -
rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] +
rho3[x1 + x3, x2, x4, x5]
};
|
In[3]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2
|
Out[3]=
|
- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5]
+ rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5]
+ rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5]
+ rho3[x1 + x5, x2, x3, x4]
|
In[4]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
|
Out[4]=
|
0
|



















=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/231c9b6d709699bf392b563aa45d79f0417696b4)


=b^{+}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{4})-b^{+}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06cd8b9b7e138b986be80a0e180a4946404b6c5d)
=b^{+}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{+}(x_{1},x_{3},x_{4})-b^{+}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{+}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e8055a80d8382baf7a0ff635102c605c27eda4b)
=b^{-}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+b^{+}(x_{1},x_{3},x_{4})-b^{+}(x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fce40ea9085985c87aecd8bb5c98ad52bce483ee)
=b^{+}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{+}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bff9ab040ba74e0c7cd17a0b5af34a4890080cc)
=b^{-}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/298ba6b42ae81403d32cd6a4b088b2957360bd25)
=b^{-}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{+}(x_{1},x_{3},x_{4})-b^{+}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e950790f43156dae93842d5adc65327387c192a5)
=b^{-}(x_{1},x_{2},x_{3})+b^{-}(x_{1}+x_{3},x_{2},x_{4})+b^{-}(x_{1},x_{3},x_{4})-b^{-}(x_{1}+x_{2},x_{3},x_{4})-b^{-}(x_{1},x_{2},x_{4})-b^{-}(x_{1}+x_{4},x_{2},x_{3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/293afcc6fc1c13efd70b97455e6723a225863a56)