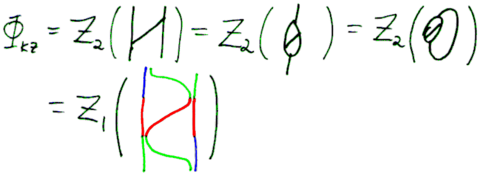The Kontsevich Integral for Knotted Trivalent Graphs

Paperlets Navigation Panel

Algebraic Knot Theory

Algebraic Knot Theory - A Call for Action.
The Kontsevich Integral for Knotted Trivalent Graphs.
Knotted Trivalent Graphs are Finitely Presented.
VS, TS and TG Algebras.
The Alexander Polynomial of a Knotted Trivalent Graph.
Some Questions About Trinions.

Finite Type Invariants

Khovanov Homology

Other

In Preparation

The information below is preliminary and cannot be trusted! (v)

Abstract

We construct a (very) well-behaved invariant of knotted trivalent graphs using only the Kontsevich integral, in three steps.

Step 1 - The Naive Kontsevich Integral

$Z_0(K)=\ \ \ \ \ \ \ \ \ \ \int\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\sum_{m;\ t_1<\ldots<t_m;\ P=\{(z_i,z'_i)\}} \frac{(-1)^{\#P_{\downarrow}}}{(2\pi i)^m} D_P \bigwedge_{i=1}^{m}\frac{dz_i-dz'_i}{z_i-z'_i}$

We define the "naive Kontsevich integral" $Z_1$ of a knotted trivalent graph or a slice thereof as in the "standard" picture above, except generalized to graphs in the obvious manner.

The Good

It has a factorization property.
For the "braid-like" factors, it has invariance under horizontal deformations.
It is morally a universal finite type invariant.

The Bad

It is divergent.

Step 2 - The Renormalized Kontsevich Integral

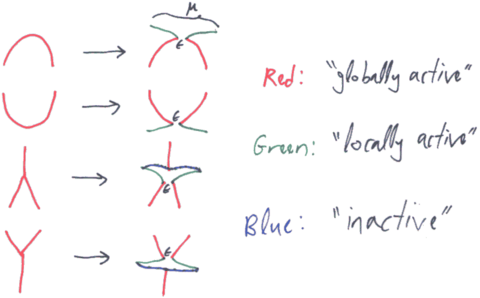
After choosing a scale $\mu$ and an infinitesimal $\epsilon$ and using ideas from renormalization theory as practiced by quantum field theorists, we define the "renormalized Kontsevich integral" $Z_2$ of a knotted trivalent graph or a slice thereof as summarized by the picture above.

The Good

It retains all the good properties of the naive Kontsevich integral.
It is convergent.
It is invariant under rigid motions of critical points and trivalent vertices.
It has sensible behaviour under vertical connect sum, delete and unzip operations.
It has a sensible behaviour under the changing of the scale $\mu$ , as follows from:

Claim. Let $w_1,\ldots,w_n$ be distinct complex numbers and let $\beta$ be another complex number. Let $B$ be the ( $n$ -strand) braid "rescaling braid" which is the image of the map $[0,1]\to[0,1]\times{\mathbb C}^n$ defined by $t\mapsto(t, e^{\beta t}w_1,\ldots,e^{\beta t}w_n)$ . Finally, in ${\mathcal A}(\uparrow_n)$ let $c$ be the "sum of all horizontal chords"; $c=\sum_{1\leq i<j\leq n}t^{ij}$ . Then up to normalization factors which we are getting right with probability $\frac{1}{2^k}$ for some small $k\in{\mathbb N}$ ,

$Z(B)=\exp\frac{\beta c}{2\pi i}\in{\mathcal A}(\uparrow_n)$ .

The Bad

It is not invariant under non-rigid motions of vertices and critical points.

Step 3 - The Corrected Kontsevich Integral

By correcting caps and cups with factors $n$ and $u$ , and the two types of trivalent vertices with factors $y$ and $\lambda$ , we define the "corrected Kontsevich integral" $Z=Z_3$ of a knotted trivalent graph or a slice thereof. It has all the good properties we can wish for. The details still need to be worked out here!