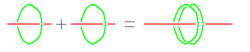The Existence of the Exponential Function
|
Introduction
The purpose of this paperlet is to use some homological algebra in order to prove the existence of a power series (with coefficients in ) which satisfies the non-linear equation
| [Main] |
as well as the initial condition
| [Init] |
Alternative proofs of the existence of are of course available, including the explicit formula . Thus the value of this paperlet is not in the result it proves but rather in the allegorical story it tells: that there is a technique to solve functional equations such as [Main] using homology. There are plenty of other examples for the use of that technique, in which the equation replacing [Main] isn't as easy (see Further Examples below). Thus the exponential function seems to be the easiest illustration of a general principle and as such it is worthy of documenting.
Thus below we will pretend not to know the exponential function and/or its relationship with the differential equation .
Acknowledgment
Significant parts of this paperlet were contributed by Omar Antolin Camarena. Further thanks to Yael Karshon, to Peter Lee and to the students of Math 1350 (2006) in general.
The Scheme
We aim to construct and solve [Main] inductively, degree by degree. Equation [Init] gives in degrees 0 and 1, and the given formula for indeed solves [Main] in degrees 0 and 1. So booting the induction is no problem. Now assume we've found a degree 7 polynomial which solves [Main] up to and including degree 7, but at this stage of the construction, it may well fail to solve [Main] in degree 8. Thus modulo degrees 9 and up, we have
| [M] |
where is the "mistake for ", a certain homogeneous polynomial of degree 8 in the variables and .
Our hope is to "fix" the mistake by replacing with , where is a degree 8 "correction", a homogeneous polynomial of degree 8 in (well, in this simple case, just a multiple of ).
| *1 The terms containing no 's make a copy of the left hand side of [M]. The terms linear in are , and . Note that since the constant term of is 1 and since we only care about degree 8, the last two terms can be replaced by and , respectively. Finally, we don't even need to look at terms higher than linear in , for these have degree 16 or more, high in the stratosphere. |
So we substitute into (a version of [Main]), expand, and consider only the low degree terms - those below and including degree 8:*1
We define a "differential" by , and the above equation becomes
| *2 It is worth noting that in some a priori sense the existence a solution of is unexpected. For must be an element of the relatively small space of power series in one variable, but the equation it is required to satisfy lives in the much bigger space of power series in two variables. Thus in some sense we have more equations than unknowns and a solution is unlikely. How fortunate we are that exponentials do exist, after all! |
To continue with our inductive construction we need to have that . Hence the existence of the exponential function hinges upon our ability to find an for which . In other words, we must show that is in the image of . This appears hopeless unless we learn more about , for the domain space of is much smaller than its target space and thus cannot be surjective, and if was in any sense "random", we simply wouldn't be able to find our correction term .*2
As we shall see momentarily by "finding syzygies", and fit within the 1st and 2nd chain groups of a rather short complex
| [Complex] |
whose first differential was already written and whose second differential is given by for any . We shall further see that for "our" , we have . Therefore in order to show that is in the image of , it suffices to show that the kernel of is equal to the image of , or simply that .
Finding a Syzygy
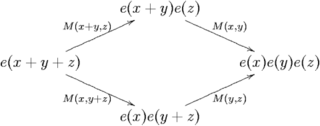
So what kind of relations can we get for ? Well, it measures how close is to turning sums into products, so we can look for preservation of properties that both addition and multiplication have. For example, they're both commutative, so we should have , and indeed this is obvious from the definition. Now let's try associativity, that is, let's compute associating first as and then as . In the first way we get
In the second we get
Comparing these two we get an interesting relation for : . Since we'll only use to find the next highest term, we can be sloppy about all but the first term of . This means that in the relation we just found we can replace by its constant term, namely 1. Upon rearranging, we get the relation promised for : .
Computing the Homology, Easy but Limited
Now let's prove that for our (piece of) chain complex. That is, letting be such that , we'll prove that for some we have .
Write the two power series as and , where the are the unknowns we wish to solve for.
The coefficient of in is
Here, is a Kronecker delta: 1 if and 0 otherwise. Since , this coefficient is zero. Multiplying by (and noting that, for example, the first term doesn't need an since the delta is only nonzero when ) we get:
| [m] |
An entirely analogous procedure tells us that the equations we must solve boil down to .
By setting in this last equation we see that . Now let and be arbitrary positive integers. This solves for most of the coefficients: . Any integer at least two can be written as , so this determines all of the for . We just need to prove that is well defined, that is, that doesn't depend on and but only on their sum.
But when and are strictly positive, the relation [m] reads , which show that we can "transfer" from one index to the other, which is what we wanted.
It only remains to find but it's easy to see this is impossible: if satisfies , then so does for any , so is arbitrary. How do our coefficient equations tell us this?
Well, we can't find a single equation for ! We've already tried taking both and to be zero, and also taking them both positive. We only have taking one zero and one positive left. Doing so gives two necessary conditions for the existence of the : for . So no comes up, and we're still not done. Fortunately setting one of and to be zero and one positive in the realtion for the does the trick.
Computing the Homology, Hard but Rewarding
Let denote the space of degree polynomials in (commuting) variables (with rational coefficients) and let be defined by , where , for and . It is easy to verify that is a chain complex, and that (for ) it agrees with the degree piece of the complex in [Complex]. We need to show that for (we don't need the vanishing of for as these degrees are covered by the initial condition [Init]). This follows from the following theorem.
Theorem. is ; otherwise .
Proof (sketch). It is easy to verify "by hand" that . For let be the th interior power of , whose th chain group is and whose differential is defined using the diagonal action of the 's. The permutation group acts on by permuting the tensor factors. If denotes the trivial representation of , then , and so
and the results readily follows. Note that the last equality uses the Eilenberg-Zilber-Künneth formula, which holds because (and especially ) is a co-simplicial space with the 's as co-face maps and with as co-degeneracies.
Further Examples
Let us briefly list a number of other places in mathematics where similar "non-linear algebraic functional equations" need to be solved. The techniques we have developed to solve [Main] can be applied in all of those cases, though sometimes it is fully successful and sometimes something breaks down somewhere along the way.
| In knot theory solving this equations is as easy as calculating 1+1=2 on an abacus:
See [Bar-Natan_Le_Thurston_03]. |
The "Duflo Homomorphism" Equation
This is the equation
written in , for an unknown where is a Lie algebra. With appropriate qualifications, , and our equation becomes the statement " is an algebra homomorphism between the invariants of and the invariants of ", and its solution is the so-called "Duflo homomorphism". This is a typical "homomorphism wanted" equation and it it has many relatives, including our primary example which is also known as the statement "the additive group of is isomorphic to the multiplicative group of ". Note that in general, the equation for being a homomorphism, say , is non-linear in the homomorphism itself.
Where from cometh the syzygies? As in the case of the exponential function, they come from the fact that for a homomorphism, associativity in the target follows from associativity in the domain.
The "Formal Quantization" Equation
This is the equation
written for an unknown "-product", within a certain complicated space of "potential products" which resembles or for some vector space . This is a typical "algebraic structure wanted" equation, in which the unknown is an "algebraic structure" (an associative product , in this case) and the equation is "the structure satisfies a law" (the associative law, in our case). Note that algebraic laws are often non-linear in the structure that they govern (the example relevant here is that the associative law is "quadratic as a function of the product"). Other examples abound, with the "structure" replaced by a "bracket" or anything else, and the "law" replaced by "Jacobi's equation" or whatever you fancy.
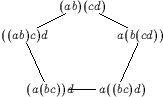
Where from cometh the syzygies? From the pentagon shown on the right.
The Drinfel'd Pentagon Equation
This is the equation
It is an equation written in some strange non-commutative algebra , for an unknown "function" which in itself lives in some non-commutative algebra . This equation is related to tensor categories, to quasi-Hopf algebras and (strange as it may seem) to knot theory, and is commonly summarized by either of the following two pictures:
This equation is a close friend of the Drinfel'd Hexagon Equation, and you can read more about both of them at [Drinfeld_90], [Drinfeld_91] and [Bar-Natan_97]. These equations have many relatives living in many further exotic spaces.
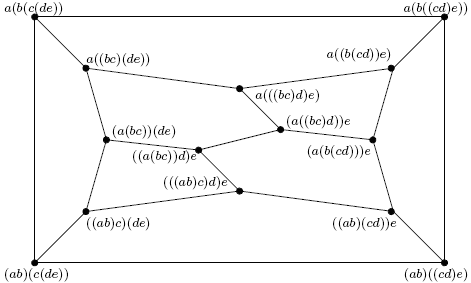
Where from cometh the syzygies? Here the equations come from the pentagon, so the syzygies must come from somewhere more complicated - the "Stasheff Polyhedron":
The Drinfel'd Twist Equation
This is the equation
This equation is written in another strange non-commutative algebra , which is a superset of . The unknown lives in some space , and and are solutions of the Drinfel'd pentagon of before. You can read more about this equation at [Drinfeld_90], [Drinfeld_91] and [Le_Murakami_96]. This equation has many relatives living in many further exotic spaces.
Where from cometh the syzygies? Again from the pentagon, but in a different way.
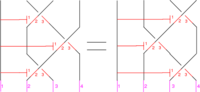
The Braidor Equation
This is the equation
written in for an unknown . It is related to the picture on the right and through it to the third Reidemeister move of braid theory and knot theory. At present, the only place to read more about it is 06-1350/Homework Assignment 4.
Where from cometh the syzygies? The third Reidemeister move comes from resolving a triple point. The corresponding syzygy comes from resolving a quadruple point. See a picture at 06-1350/Homework Assignment 4.
Further Further Examples
This subsection is by definition forever empty, for if a worthwhile further further example comes to mind, mine or yours, it should be added as a subsection right above.
References
[Bar-Natan_97] ^ D. Bar-Natan, Non-associative tangles, in Geometric topology (proceedings of the Georgia international topology conference), (W. H. Kazez, ed.), 139-183, Amer. Math. Soc. and International Press, Providence, 1997.
[Bar-Natan_Le_Thurston_03] ^ D. Bar-Natan, T. Q. T. Le and D. P. Thurston, Two applications of elementary knot theory to Lie algebras and Vassiliev invariants, Geometry and Topology 7-1 (2003) 1-31, arXiv:math.QA/0204311.
[Drinfeld_90] ^ V. G. Drinfel'd, Quasi-Hopf algebras, Leningrad Math. J. 1 (1990) 1419-1457.
[Drinfeld_91] ^ V. G. Drinfel'd, On quasitriangular Quasi-Hopf algebras and a group closely connected with , Leningrad Math. J. 2 (1991) 829-860.
[Le_Murakami_96] ^ T. Q. T. Le and J. Murakami, The universal Vassiliev-Kontsevich invariant for framed oriented links, Compositio Math. 102 (1996), 41-64, arXiv:hep-th/9401016.
























![{\displaystyle d:{\mathbb {Q} }[x]\to {\mathbb {Q} }[x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67d6cccdf4c96e839554d2b513209c62fc96970d)



![{\displaystyle {\mathbb {Q} }[[x]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2126d26f3c43437059116c824ec12b1cc3ea099)
![{\displaystyle {\mathbb {Q} }[[x,y]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef877f7f4f51bf5a0da425e2dbbff573d13c3d5b)



![{\displaystyle \left(\epsilon \in C^{1}={\mathbb {Q} }[[x]]\right)\longrightarrow \left(M\in C^{2}={\mathbb {Q} }[[x,y]]\right)\longrightarrow \left(C^{3}={\mathbb {Q} }[[x,y,z]]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5907f397d3978c3c9ee66844146570f83e661e5)

![{\displaystyle m\in {\mathbb {Q} }[[x,y]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5a97f89d61e5946dbff1f26f3521d0795e5c6f9)












![{\displaystyle M(x,y)\in \mathbb {Q} [[x,y]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232aea0f2e2ed904713db1e8061ac445c6c70cd6)
![{\displaystyle \epsilon (x)\in \mathbb {Q} [[x]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59dff8498d6c5bad3bc2af7814e5b64bf65218cc)