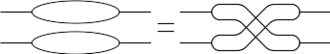The Envelope of The Alexander Polynomial
|
The information below is preliminary and cannot be trusted! (v)
The Internal Kernel of the Alexander Polynomial
All that there is here comes from 06-1350/Class Notes for Tuesday October 24. Many further relevant facts are in arXiv:q-alg/9602014 by José M. Figueroa-O'Farrill, Takashi Kimura, Arkady Vaintrob and in arXiv:math.QA/0204346 by Jens Lieberum.
At the moment I know of just three relations in the internal kernel of the Alexander polynomial: the bubble relation, the H relation and the 4Y relation:
I have good reasons to suspect that there are further relations. But at the moment I don't know what they are, so below we will make do with what we have.
The VS-Algebra Envelope of the Alexander Polynomial
Alexander-Conway, Precisely
Let denote the Conway polynomial and denote the Alexander polynomial. By [Bar-Natan_Garoufalidis_96] we know that
is a canonical Vassiliev power series. Let denote "half a bubble". The following theorem follows easily from the above canonicity statement and the fact that (in shorter and less precise form, ), where is the weight system of the Alexander-Conway polynomial:
Theorem. Let be a knot and let be the Kontsevich integral of . Then within the envelope of the Alexander-Conway polynomial,
References
[Bar-Natan_Garoufalidis_96] ^ Dror Bar-Natan and Stavros Garoufalidis, On the Melvin-Morton-Rozansky Conjecture, Inventiones Mathematicae 125 (1996) 103-133.