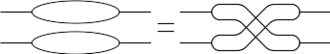The Envelope of The Alexander Polynomial: Difference between revisions
No edit summary |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{Paperlets Navigation}} |
{{Paperlets Navigation}} |
||
{{In Preparation}} |
|||
==The Internal Kernel of the Alexander Polynomial== |
==The Internal Kernel of the Alexander Polynomial== |
||
All that there is here comes from [[06-1350/Class Notes for Tuesday October 24]]. Many further relevant facts are in {{arXiv|q-alg/9602014}} by José M. Figueroa-O'Farrill, Takashi Kimura, Arkady Vaintrob and in {{arXiv|math.QA/0204346}} by Jens Lieberum. |
|||
At the moment I know of just three relations in the internal kernel of the Alexander polynomial: the bubble relation, the H relation and the 4Y relation: |
|||
[[Image:The Bubble Relation.svg|thumb|330px|center|The Bubble Relation]] |
|||
[[Image:TheHRelation.svg|thumb|550px|center|The H Relation]] |
|||
[[Image:The 4Y Relation.svg|thumb|440px|center|The 4Y Relation]] |
|||
I have good reasons to suspect that there are further relations. But at the moment I don't know what they are, so below we will make do with what we have. |
|||
==The VS-Algebra Envelope of the Alexander Polynomial== |
==The VS-Algebra Envelope of the Alexander Polynomial== |
||
==Alexander-Conway, Precisely== |
|||
Let <math>C(z)</math> denote the Conway polynomial and <math>A(t)</math> denote the Alexander polynomial. By {{ref|Bar-Natan_Garoufalidis_96}} we know that |
|||
{{Equation*|<math>\frac{\hbar}{e^{\hbar/2}-e^{-\hbar/2}}C(e^{\hbar/2}-e^{-\hbar/2}) = \frac{\hbar}{e^{\hbar/2}-e^{-\hbar/2}}A(e^\hbar)</math>}} |
|||
is a canonical Vassiliev power series. Let <math>d</math> denote "half a bubble". The following theorem follows easily from the above canonicity statement and the fact that <math>W_C(d^{2n})=(-2\hbar^2)^n</math> (in shorter and less precise form, <math>\hbar=W_C(id/\sqrt2)</math>), where <math>W_C</math> is the weight system of the Alexander-Conway polynomial: |
|||
'''Theorem.''' Let <math>K</math> be a knot and let <math>Z(K)</math> be the Kontsevich integral of <math>K</math>. Then within the envelope of the Alexander-Conway polynomial, |
|||
{{Equation*|<math>Z(K) = \frac{id/\sqrt2}{e^{id/2\sqrt2}-e^{-id/2\sqrt2}} C(e^{id/2\sqrt2}-e^{-id/2\sqrt2}) = \frac{id/\sqrt2}{e^{id/2\sqrt2}-e^{-id/2\sqrt2}} A(e^{id/\sqrt2})</math>.}} |
|||
==References== |
|||
{{note|Bar-Natan_Garoufalidis_96}} Dror Bar-Natan and Stavros Garoufalidis, ''[http://www.math.toronto.edu/~drorbn/LOP.html#MMR On the Melvin-Morton-Rozansky Conjecture],'' Inventiones Mathematicae '''125''' (1996) 103-133. |
|||
Latest revision as of 09:13, 1 May 2007
|
The information below is preliminary and cannot be trusted! (v)
The Internal Kernel of the Alexander Polynomial
All that there is here comes from 06-1350/Class Notes for Tuesday October 24. Many further relevant facts are in arXiv:q-alg/9602014 by José M. Figueroa-O'Farrill, Takashi Kimura, Arkady Vaintrob and in arXiv:math.QA/0204346 by Jens Lieberum.
At the moment I know of just three relations in the internal kernel of the Alexander polynomial: the bubble relation, the H relation and the 4Y relation:
I have good reasons to suspect that there are further relations. But at the moment I don't know what they are, so below we will make do with what we have.
The VS-Algebra Envelope of the Alexander Polynomial
Alexander-Conway, Precisely
Let denote the Conway polynomial and denote the Alexander polynomial. By [Bar-Natan_Garoufalidis_96] we know that
is a canonical Vassiliev power series. Let denote "half a bubble". The following theorem follows easily from the above canonicity statement and the fact that (in shorter and less precise form, ), where is the weight system of the Alexander-Conway polynomial:
Theorem. Let be a knot and let be the Kontsevich integral of . Then within the envelope of the Alexander-Conway polynomial,
References
[Bar-Natan_Garoufalidis_96] ^ Dror Bar-Natan and Stavros Garoufalidis, On the Melvin-Morton-Rozansky Conjecture, Inventiones Mathematicae 125 (1996) 103-133.