Fields 2009 Finite Type Invariants Proposal
This is a part of a proposal for a 2009 Knot Theory Program at the Fields Institute.
What is a Universal Finite Type Invariant?
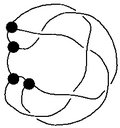
Given a graph ("the skeleton"), let denote the set of all "knottings" of - the set of all embeddings of into considered modulo isotopy. So if is a circle, is an ordinary knot. If it is a union of circles, is a link, and if it is, say, a tetrahedron, will contain, for example, the knotted graph shown on the right.
A universal finite type invariant (using a rather broad definition) is a family of invariants , one for each skeleton , valued in some specific family of linear spaces one for each . The spaces are themselves defined in terms of graphs along with some linear algebra, but since we don't need the details here, we won't show them. A certain "universality" property is expected to hold, but again, we don't need it right now so we won't discuss it.