| Additions to this web site no longer count towards good deed points.
|
| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 10
|
About This Class.  Monday: Introduction and the Brachistochrone. Monday: Introduction and the Brachistochrone.  Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes. Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes.  Friday: Some basic techniques: first order linear equations. Friday: Some basic techniques: first order linear equations.
|
| 2
|
Sep 17
|
 Monday: Separated equations, escape velocities. HW1. Monday: Separated equations, escape velocities. HW1.  Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations. Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations.  Friday: Reverse engineering separated and exact equations. Friday: Reverse engineering separated and exact equations.
|
| 3
|
Sep 24
|
 Monday: Solving exact equations, integration factors. HW2. Monday: Solving exact equations, integration factors. HW2.  Tuesday: Statement of the Fundamental Theorem. Class Photo. Tuesday: Statement of the Fundamental Theorem. Class Photo.  Friday: Proof of the Fundamental Theorem. Friday: Proof of the Fundamental Theorem.
|
| 4
|
Oct 1
|
 Monday: Last notes on the fundamental theorem. HW3. Monday: Last notes on the fundamental theorem. HW3.  Tuesday Hour 1: The chain law, examples of variational problems. Tuesday Hour 1: The chain law, examples of variational problems.  Tuesday Hour 2: Deriving Euler-Lagrange. Tuesday Hour 2: Deriving Euler-Lagrange.  Friday: Reductions of Euler-Lagrange. Friday: Reductions of Euler-Lagrange.
|
| 5
|
Oct 8
|
Monday is thanksgiving.  Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4. Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4.  Friday: More Lagrange multipliers, numerical methods. Friday: More Lagrange multipliers, numerical methods.
|
| 6
|
Oct 15
|
 Monday: Euler and improved Euler. Monday: Euler and improved Euler.  Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods. Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods.  Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs. Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs.
|
| 7
|
Oct 22
|
 Monday: Multiple roots, reduction of order, undetermined coefficients. Monday: Multiple roots, reduction of order, undetermined coefficients.  Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday. Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday.
|
| 8
|
Oct 29
|
 Monday: The basic properties of matrix exponentiation. Monday: The basic properties of matrix exponentiation.  Tuesday: Matrix exponentiation: examples. Tuesday: Matrix exponentiation: examples.  Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class
|
| 9
|
Nov 5
|
 Monday: Non-homogeneous systems. Monday: Non-homogeneous systems.  Tuesday: The Catalan numbers, power series, and ODEs. Tuesday: The Catalan numbers, power series, and ODEs.  Friday: Global existence for linear ODEs, the Wronskian. Friday: Global existence for linear ODEs, the Wronskian.
|
| 10
|
Nov 12
|
Monday-Tuesday is UofT November break. HW7.  Friday: Series solutions for Friday: Series solutions for  . .
|
| 11
|
Nov 19
|
 Monday: Monday:  is irrational, more on the radius of convergence. is irrational, more on the radius of convergence.  Tuesday (class): Airy's equation, Fuchs' theorem. Tuesday (class): Airy's equation, Fuchs' theorem.  Tuesday (tutorial): Regular singular points. HW8. Tuesday (tutorial): Regular singular points. HW8.  Friday: Discussion of regular singular points.. Friday: Discussion of regular singular points..
|
| 12
|
Nov 26
|
 Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF). Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF).  Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9. Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9.  Friday: Non-oscillation, Sturm comparison. Friday: Non-oscillation, Sturm comparison.
|
| 13
|
Dec 3
|
 Monday: More Sturm comparisons, changing the independent variable. Monday: More Sturm comparisons, changing the independent variable.  Tuesday: Amplitudes of oscillations. Last class was on Tuesday! Tuesday: Amplitudes of oscillations. Last class was on Tuesday!
|
| F1
|
Dec 10
|
|
| F2
|
Dec 17
|
The Final Exam (time, place, style, office hours times)
|
| Register of Good Deeds
|

Add your name / see who's in!
|
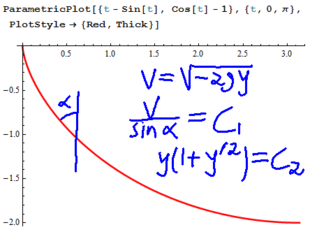
|
|
Disclamer: This is a student prepared note based on the lecures of Friday, September 28th and Monday October 1st.
Lipschitz
Def.  is called Lipschitz if
is called Lipschitz if  (a Lipschitz constant of f) such that
(a Lipschitz constant of f) such that  .
.
Note that any function that is Lipschitz is uniformly continuous, and that if a function f and its derivative are both continous on a compact set then f is Lipschitz.
Statement of Existence and Uniqueness Theorem
Thm. Existence and Uniqueness Theorem for ODEs
Let ![{\displaystyle f:\mathbb {R} =[x_{0}-a,x_{0}+a]\times [y_{0}-b,y_{0}+b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ceefbacbba0b01a08d8e3103c276c2d5a64c6554) be continuous and uniformly Lipschitz relative to y. Then the equation
be continuous and uniformly Lipschitz relative to y. Then the equation  with
with  has a unique solution
has a unique solution ![{\displaystyle \Phi :[x_{0}-\delta ,x_{0}+\delta ]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d96fbff31d79448da931b55140e70908fd554b65) where
where  where M is a bound of f on
where M is a bound of f on  .
.
Proof of Existence
This is proven by showing the equation  exists, given the noted assumptions.
exists, given the noted assumptions.
Let  and let
and let  . IF we can prove the following three claims, we have proven the theorem. The proofs of these claims will follow below.
. IF we can prove the following three claims, we have proven the theorem. The proofs of these claims will follow below.
Claim 1:  is well-defined. More precisely,
is well-defined. More precisely,  is continuous and
is continuous and ![{\displaystyle \forall x\in [x_{0}-\delta ,x_{0}+\delta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36fcf8a6a17499c767e8af66e2450dae5a8f441e) ,
,  where b is as referred to above.
where b is as referred to above.
Claim 2: For  ,
,  .
.
Claim 3: if  is a series of functions such that
is a series of functions such that  , with
, with  equal to some finite number, then
equal to some finite number, then  converges uniformly to some function
converges uniformly to some function 
Using these three claims, we have shown that the solution  exists.
exists.
Proofs of Claims
Proof of Claim 1:
The statement is trivially true for  . Assume the claim is true for
. Assume the claim is true for  .
.  is continuous, being the integral of a continuous function.
is continuous, being the integral of a continuous function.








Proof of Claim 2:








Note that the sequence  has
has  equal to some finite number.
equal to some finite number.
Proof of Claim 3: Assigned in Homework 3, Task 1, see page for solutions.
Proof of Uniqueness
Suppose  and
and  are both solutions. Let
are both solutions. Let  .
.

We have that  for some constant k, which means
for some constant k, which means  , and that
, and that  .
.
Let  . Note that
. Note that  as in this case we are integrating over an empty set, and that U thus defined has
as in this case we are integrating over an empty set, and that U thus defined has  . Then
. Then

Then  , and
, and  .
.




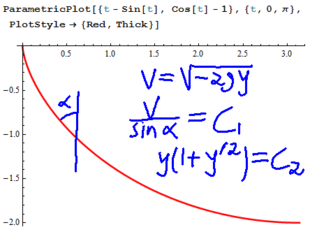



![{\displaystyle f:\mathbb {R} =[x_{0}-a,x_{0}+a]\times [y_{0}-b,y_{0}+b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ceefbacbba0b01a08d8e3103c276c2d5a64c6554)


![{\displaystyle \Phi :[x_{0}-\delta ,x_{0}+\delta ]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d96fbff31d79448da931b55140e70908fd554b65)






![{\displaystyle \forall x\in [x_{0}-\delta ,x_{0}+\delta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36fcf8a6a17499c767e8af66e2450dae5a8f441e)





































