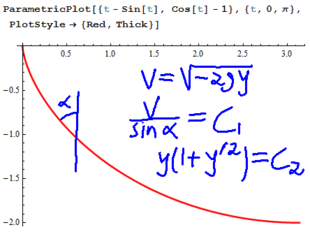12-267
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Advanced Ordinary Differential Equations
Department of Mathematics, University of Toronto, Fall 2012
Agenda: If calculus is about change, differential equations are the equations governing change. We'll learn much about these, and nothing's more important!
Instructor: Dror Bar-Natan, drorbn@math.toronto.edu, Bahen 6178, 416-946-5438. Office hours: by appointment.
Classes: Mondays, Tuesdays, and Fridays 9-10 in RW 229.
| Teaching Assistant: Jordan Bell, jordan.bell@utoronto.ca.
Tutorials: Tuesdays 10-11 at RW 229. No tutorials on the first week of classes. |
Text
Boyce and DiPrima, Elementary Differential Equations and Boundary Value Problems (current edition is 9th and 10th will be coming out shortly. Hopefully any late enough edition will do).
Further Resources
- Also previously taught by T. Bloom, C. Pugh, D. Remenik.
- My 12-267 notebook.
| Dror's notes above / Student's notes below |
Solving the complicated integral in the Brachistochroe integral
integral sqrt((d-y)/y) dy = integral sqrt(d y-y^2)/y dy
For the integrand sqrt(d y-y^2)/y, complete the square:
= integral sqrt(d^2/4-(y-d/2)^2)/y dy
For the integrand sqrt(d^2/4-(y-d/2)^2)/y, substitute u = y-d/2 and du = dy:
= integral (2 sqrt(d^2/4-u^2))/(d+2 u) du = 2 integral sqrt(d^2/4-u^2)/(d+2 u) du
For the integrand sqrt(d^2/4-u^2)/(d+2 u), (assuming all variables are positive) substitute u = 1/2 d sin(s) and du = 1/2 d cos(s) ds. Then sqrt(d^2/4-u^2) = sqrt(d^2/4-1/4 d^2 sin^2(s)) = 1/2 d cos(s) and s = sin^(-1)((2 u)/d):
= d^2/2 integral (cos^2(s))/(d sin(s)+d) ds
For the integrand (cos^2(s))/(d sin(s)+d), substitute p = tan(s/2) and dp = 1/2 sec^2(s/2) ds. Then transform the integrand using the substitutions sin(s) = (2 p)/(p^2+1), cos(s) = (1-p^2)/(p^2+1) and ds = (2 dp)/(p^2+1):
= d^2/2 integral (2 (1-p^2)^2)/((p^2+1)^3 ((2 d p)/(p^2+1)+d)) dp
Simplify the integrand (2 (1-p^2)^2)/((p^2+1)^3 ((2 d p)/(p^2+1)+d)) to get (2 (p-1)^2)/(d p^4+2 d p^2+d):
= d^2/2 integral (2 (p-1)^2)/(d p^4+2 d p^2+d) dp = d^2 integral (p-1)^2/(d p^4+2 d p^2+d) dp = d^2 integral (p-1)^2/(d (p^2+1)^2) dp = d integral (p-1)^2/(p^2+1)^2 dp
For the integrand (p-1)^2/(p^2+1)^2, use partial fractions:
= d integral (1/(p^2+1)-(2 p)/(p^2+1)^2) dp = d integral 1/(p^2+1) dp-2 d integral p/(p^2+1)^2 dp
For the integrand p/(p^2+1)^2, substitute w = p^2+1 and dw = 2 p dp:
= d integral 1/(p^2+1) dp-d integral 1/w^2 dw
The integral of 1/(p^2+1) is tan^(-1)(p):
= d tan^(-1)(p)-d integral 1/w^2 dw = d tan^(-1)(p)+d/w+constant
Substitute back for w = p^2+1:
= (d ((p^2+1) tan^(-1)(p)+1))/(p^2+1)+C
Substitute back for p = tan(s/2):
= 1/2 d (cos(s)+2 tan^(-1)(tan(s/2))+1)+C
Substitute back for s = sin^(-1)((2 u)/d):
= 1/2 (sqrt(d^2-4 u^2)+2 d tan^(-1)((2 u)/(d (sqrt(1-(4 u^2)/d^2)+1)))+d)+C
Substitute back for u = y-d/2:
= d (-tan^(-1)((d-2 y)/(2 d sqrt((y (d-y))/d^2)+d)))+sqrt(y (d-y))+d/2+C
Factor the answer a different way:
= 1/2 (-2 d tan^(-1)((d-2 y)/(2 d sqrt((y (d-y))/d^2)+d))+2 sqrt(y (d-y))+d)+C
Which is equivalent for restricted y and d values to:
= y sqrt(d/y-1)-1/2 d tan^(-1)((sqrt(d/y-1) (d-2 y))/(2 (d-y)))+C Syjytg 23:00, 11 September 2012 (EDT)