0708-1300/justforfun6
We can see that the linking number of any pair of components in is non zero while there is a pair of components of having linking number zero. For this we need to find a practical way to compute the linking number but this comes with the solution of problem 4.3 of this homework.
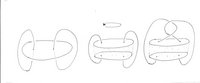
On the other hand, to see that the complements of these links are diffeomorphic look at the following figure.
In the first part of the figure we can see the complement of . Cut this along the disc which boundary is the horizontal circle and you will get something similar to the middle figure. The space that you see between the two discs is not space it is complete emptiness. Rotate the upper disc as indicated by the arrow and you will get the right part of the figure. Finally glue again the two discs and you will get the link .
This cut-and-pasting gives us a (maybe non-smooth) homeomorphism but, using the trick of immersing Failed to parse (unknown function "\mathb"): {\displaystyle \mathb{R}^3} in , using that this is compact to find a deformation of our map that is smooth we will get the desired diffeomorphism. Or even more simple, if a good drawer paints this picture again it will certainly be smooth enough.