
Add your name / see who's in!
|
| #
|
Week of...
|
Links
|
| Fall Semester
|
| 1
|
Sep 10
|
About, Tue, Thu
|
| 2
|
Sep 17
|
Tue, HW1, Thu
|
| 3
|
Sep 24
|
Tue, Photo, Thu
|
| 4
|
Oct 1
|
Questionnaire, Tue, HW2, Thu
|
| 5
|
Oct 8
|
Thanksgiving, Tue, Thu
|
| 6
|
Oct 15
|
Tue, HW3, Thu
|
| 7
|
Oct 22
|
Tue, Thu
|
| 8
|
Oct 29
|
Tue, HW4, Thu, Hilbert sphere
|
| 9
|
Nov 5
|
Tue,Thu, TE1
|
| 10
|
Nov 12
|
Tue, Thu
|
| 11
|
Nov 19
|
Tue, Thu, HW5
|
| 12
|
Nov 26
|
Tue, Thu
|
| 13
|
Dec 3
|
Tue, Thu, HW6
|
| Spring Semester
|
| 14
|
Jan 7
|
Tue, Thu, HW7
|
| 15
|
Jan 14
|
Tue, Thu
|
| 16
|
Jan 21
|
Tue, Thu, HW8
|
| 17
|
Jan 28
|
Tue, Thu
|
| 18
|
Feb 4
|
Tue
|
| 19
|
Feb 11
|
TE2, Tue, HW9, Thu, Feb 17: last chance to drop class
|
| R
|
Feb 18
|
Reading week
|
| 20
|
Feb 25
|
Tue, Thu, HW10
|
| 21
|
Mar 3
|
Tue, Thu
|
| 22
|
Mar 10
|
Tue, Thu, HW11
|
| 23
|
Mar 17
|
Tue, Thu
|
| 24
|
Mar 24
|
Tue, HW12, Thu
|
| 25
|
Mar 31
|
Referendum,Tue, Thu
|
| 26
|
Apr 7
|
Tue, Thu
|
| R
|
Apr 14
|
Office hours
|
| R
|
Apr 21
|
Office hours
|
| F
|
Apr 28
|
Office hours, Final (Fri, May 2)
|
| Register of Good Deeds
|
| Errata to Bredon's Book
|
|
Announcements go here
Reading
Read, reread and rereread your notes to this point, and make sure that you really, really really, really really really understand everything in them. Do the same every week!
Doing
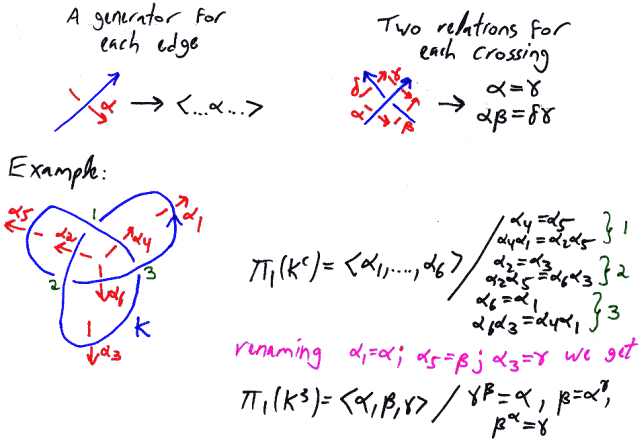
Just one problem. Let  be a knot in
be a knot in  presented by a planar diagram
presented by a planar diagram  . With a massive use of Van-Kampen's theorem, show that the fundamental group of the complement of
. With a massive use of Van-Kampen's theorem, show that the fundamental group of the complement of  has a presentation (the "Wirtinger" presentation) with one generator for each edge of
has a presentation (the "Wirtinger" presentation) with one generator for each edge of  and two relations for each crossing of
and two relations for each crossing of  , as indicated in the figure below.
, as indicated in the figure below.
Due Date
This assignment is due in class on Thursday February 7, 2008.




