0708-1300/Class notes for Tuesday, October 16: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{0708-1300/Navigation}} |
{{0708-1300/Navigation}} |
||
==Dror's Computer Program for C+<math>\alpha</math> C== |
|||
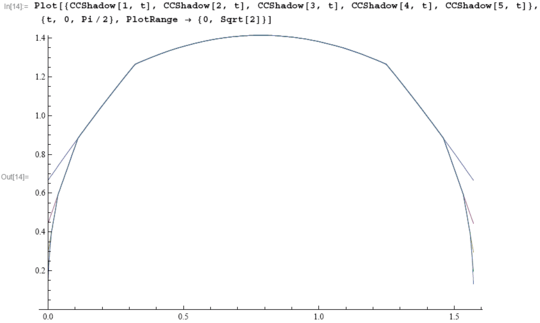
Our handout today is a printout of a Mathematica notebook that computes the measure of the projection of <math>C\times C</math> in a direction <math>t\in[0,\pi/2]</math> (where <math>C</math> is the standard Cantor set). Here's the {{Home Link|classes/0708/GeomAndTop/CCShadow.nb|notebook}}, and here's a {{Home Link|classes/0708/GeomAndTop/CCShadow.pdf|PDF}} version. Also, here's the main picture on that notebook: |
Our handout today is a printout of a Mathematica notebook that computes the measure of the projection of <math>C\times C</math> in a direction <math>t\in[0,\pi/2]</math> (where <math>C</math> is the standard Cantor set). Here's the {{Home Link|classes/0708/GeomAndTop/CCShadow.nb|notebook}}, and here's a {{Home Link|classes/0708/GeomAndTop/CCShadow.pdf|PDF}} version. Also, here's the main picture on that notebook: |
||
[[Image:0708-1300-CCShadow.png|center|540px]] |
[[Image:0708-1300-CCShadow.png|center|540px]] |
||
==Typed Class Notes - First Hour== |
|||
'''Today's Agenda:''' |
|||
Proof of Sard's Theorem. That is, for <math>f:M^m\rightarrow N^n</math> being smooth, the measure <math>\mu</math>(critical values of f) = 0. |
|||
'''Comments regarding last class''' |
|||
1) In our counterexample to Sard's Theorem for the case of <math>C^1</math> functions it was emphasized that there are functions f from ''a'' Cantor set C' to ''the'' Cantor set C. We then let <math>g(x,y) = f(x) + f(y)</math> and hence the critical values are <math>C+C = [0,2]</math> as was shown last time. The sketch of such an f was the same as last class. |
|||
Furthermore, in general we can find a <math>C^n</math> such function where we make the "bumps" in f smoother as needed and so <math>f(C') = C''</math> where <math>C''</math> is a "very thin" Cantor set. But now let <math>g(x,y,z,\ldots) = f(x) + f(y) + f(z) +\ldots</math> which will have an image of <math>C'' + C'' + C'' + \ldots =</math> an interval. |
|||
2) The code, and what the program does, for Dror's program (above) was described. It is impractical to describe it here in detail and so I will only comment that it computes the measure of <math>C+\alpha C</math> for various alpha and that the methodology relied on the 2nd method of proof regarding C+C done last class. |
|||
'''Proof of Sard's Theorem''' |
|||
Firstly, it is enough to argue locally. |
|||
Further, the technical assumption about manifolds that until now has been largely ignored is that our M must be second countable. Recall that this means that there is a countable basis for the topology on M. |
|||
As a counterexample to Sard's Theorem when M is NOT second countable consider the real line with the discrete topology, a zero dimensional manifold, mapping via the identity onto the real line with the normal topology. Every point in the real line is thus a critical point and the real line has non zero measure. |
|||
We can restrict our neighborhoods so that we can assume <math>M=\mathbb{R}^m</math> and <math>N=\mathbb{R}^n</math> |
|||
The general idea here is that if we consider a function g=f' that is nonzero at p but that f is zero at p, the inverse image is (in some chart) a straight line (a manifold). As such, we will inductively reduce the dimension from m down to zero. For m=0 there is nothing to prove. Hence we assume true for m-1. |
|||
Now, set <math>D_k = \{p |</math> all partial derivities of f of order <math>\leq k\}</math> for <math>k\geq 1</math> |
|||
Set <math>D_0 = \{p\ |\ df_p</math> is not onto }. This is just the critical points. |
|||
Clearly <math>D_0\supset D_1\supset\ldots\supset D_i\supset\ldots\supset D_m</math> |
|||
We will show by backwards induction that <math>\mu(F(D_k)) = 0</math> |
|||
''Comment:'' |
|||
We have not actually defined the measure <math>\mu</math>. We use it merely to denote that <math>F(D_k))</math> has measure zero, a concept that we DID define. |
|||
'''Claim 1''' |
|||
<math>F(D_m)</math> has measure 0. |
|||
''Proof'' |
|||
W.L.O.G (without loss of generality) we can assume n=1. Intuitively this is reasonable as in lower dimensions the theorem is harder to prove; indeed, a set of size <math>\epsilon</math> in 1D becomes a smaller set of size <math>\epsilon^2</math> in 2D etc. More precisely, for <math>f = (f_1,\ldots,f_n)</math>, <math>f(D_n)\subset f_1(D_m)\times{R}^{n-1}</math>. Applying the proposition that if A is of measure zero in <math>\mathbb{R}</math> then <math>A\times\mathbb{R}^{n-1}</math> is measure zero in <math>\mathbb{R}^n</math> we now see that assuming n=1 is justified. |
|||
''Reminder'' |
|||
Taylor's Theorem: for smooth enough <math>g:\mathbb{R}\rightarrow\mathbb{R}</math> and some <math>x_0</math> then <math>g(x) = \sum_{j=0}^{m} \frac{g^{(j)}(x_0)}{j!}(x-x_0)^j + \frac{g^{(m+1)}(t)}{(m+1)!}(x-x_0)^{m+1}</math> |
|||
for some t between x and <math>x_0</math>. |
|||
For <math>x_0\in D_m</math> all but the last term vanishes and so we can conclude that f(x) is bounded by a constant times <math>(x-x_0)^{m+1}</math>. |
|||
Now let us consider a box B in <math>\mathbb{R}^m</math> containing a section of <math>D_m</math>. We divide B into <math>C_1\lambda^m</math> boxes of side <math>1/\lambda</math>. |
|||
By Taylor's Theorem, <math>f(B_i)\subset</math> of an interval of length <math>C_2\frac{1}{\lambda^{m+1}}</math> where the constant <math>C_2</math> is determined by Taylor's Theorem. Call this interval <math>I_i</math> |
|||
Hence, |
|||
<math>f(D_m)\subset\bigcup_{i:B_i\cap D_m \neq 0} f(B_i)\subset \bigcup_{i:B_i\cap D_m \neq 0}I_i</math> |
|||
But <math>\sum_{i} length(I_i)\leq C_1\lambda^m C_2\frac{1}{\lambda^{m+1}}</math> which tends to zero as <math>\lambda</math> tends to infinity. |
|||
''Q.E.D for Claim 1'' |
|||
'''Claim 2''' |
|||
<math>f(D_k)</math> has measure zero for <math>k\geq 1</math>. We just proved this for k=m. |
|||
Now, W.L.O.G. <math>D_{k+1}</math> is the empty set. If not, just consider <math>M^m - D_{k+1}</math> which is still a manifold as <math>D_{k+1}</math> is closed (as it is determined by the "closed" condition that a determinant equals zero) |
|||
So, there is some kth derivative g of f such that <math>dg\neq 0</math>. |
|||
So <math>D_k\subset g^{-1}(0)</math> but <math>g^{-1}(0)</math> is at least locally a manifold of dimension 1 less. So, <math>f(D_k)\subset f(D_k\cap g^{-1}(0)</math> which has measure zero due to our induction hypothesis. |
|||
''Q.E.D for Claim 2'' |
|||
'''Claim 3''' |
|||
<math>f(D_0)</math> is of measure zero. |
|||
Recall <math>D_0</math> is defined differently from the <math>D_k</math> and so requires a different technique to prove. |
|||
W.L.O.G. lets assume that <math>D_1</math> is the empty set. So, some derivative of f is not zero. W.L.O.G. <math>\frac{\partial f_1}{\partial x_1}</math> is non zero near some point p. We can simply move to a coordinate system where this is true. |
|||
The idea here is to prove that the intersection with any "slice" has measure zero where we will then invoke a theorem that will claim everything has measure zero. |
|||
So, let U be an open neighborhood of a point <math>p\in M</math>. Consider <math>f_1:U\rightarrow\mathbb{R}</math> and let <math>df_1</math> be onto. Using our previous theorem for the local structure of such a submersion W.L.O.G. let us assume <math>f_1:\mathbb{R}^m\rightarrow\mathbb{R}</math> via <math>(x_1,\ldots,x_m)\mapsto x_1</math>. That is, <math>f_1 = x_1</math>. |
|||
Our differential df then is just the matrix whose first row consists of <math>(1,0,\ldots,0)</math>. Then df is onto if the submatrix consisting of all but the first row and first column is invertible. |
|||
For notational convenience let us say <math>f =(f_1,f_{rest})</math>. |
|||
Now define <math>U_t = \{t\times\mathbb{R}^{m-1}\}</math> |
|||
Also lets denote "critical points of f'' by CP(f) and "critical values of f" by CV(f) |
|||
'''Claim 4''' |
|||
The <math>CP(f) = \bigcup_{t\in\mathbb{R}}\{t\}\times CP(f_{rest}|_{U_t})</math> |
|||
<math>\Rightarrow</math> |
|||
<math>CV(f) = \bigcup_{t\in\mathbb{R}}\{t\}\times CV(f_{rest}|_{U_t})</math>. |
|||
But <math>CV(f_{rest}|_{U_t})</math> has measure zero by our induction. |
|||
'''Lemma 1''' |
|||
If <math>A\subset I^2</math> is closed and has <math>\mu(A\cap(\{t\}\times I)) = 0\ \forall t</math> |
|||
then <math>\mu(A)=0</math>. |
|||
''Proof'' |
|||
Note: We prove this significantly differently then in Bredon |
|||
''Sublemma'' |
|||
If <math>\{t\}\times U</math> for an open U cover <math>\{t\}\times I\cap A</math> for a closed A then <math>\exists\epsilon>0</math> such that <math>(t-\epsilon,t+\epsilon)\times U\supset (t-\epsilon,t+\epsilon)\times I\cap A</math> |
|||
Indeed, let <math>d:A-(I\times U)\rightarrow\mathbb{R}</math> be <math>d(x) = |x_1-t|</math> then d is a continuous function of a compact set and so obtains a minimum and since d>0 then <math>min(d)>0 \rightarrow d>\epsilon>0</math>. But this <math>\epsilon</math> works for the claim. ''Q.E.D'' |
|||
''The rest of the proof of Lemma 1, and of Sard's Theorem will be left until next class'' |
|||
Revision as of 13:44, 16 October 2007
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dror's Computer Program for C+ C
Our handout today is a printout of a Mathematica notebook that computes the measure of the projection of in a direction (where is the standard Cantor set). Here's the notebook, and here's a PDF version. Also, here's the main picture on that notebook:
Typed Class Notes - First Hour
Today's Agenda:
Proof of Sard's Theorem. That is, for being smooth, the measure (critical values of f) = 0.
Comments regarding last class
1) In our counterexample to Sard's Theorem for the case of functions it was emphasized that there are functions f from a Cantor set C' to the Cantor set C. We then let and hence the critical values are as was shown last time. The sketch of such an f was the same as last class.
Furthermore, in general we can find a such function where we make the "bumps" in f smoother as needed and so where is a "very thin" Cantor set. But now let which will have an image of an interval.
2) The code, and what the program does, for Dror's program (above) was described. It is impractical to describe it here in detail and so I will only comment that it computes the measure of for various alpha and that the methodology relied on the 2nd method of proof regarding C+C done last class.
Proof of Sard's Theorem
Firstly, it is enough to argue locally.
Further, the technical assumption about manifolds that until now has been largely ignored is that our M must be second countable. Recall that this means that there is a countable basis for the topology on M.
As a counterexample to Sard's Theorem when M is NOT second countable consider the real line with the discrete topology, a zero dimensional manifold, mapping via the identity onto the real line with the normal topology. Every point in the real line is thus a critical point and the real line has non zero measure.
We can restrict our neighborhoods so that we can assume and
The general idea here is that if we consider a function g=f' that is nonzero at p but that f is zero at p, the inverse image is (in some chart) a straight line (a manifold). As such, we will inductively reduce the dimension from m down to zero. For m=0 there is nothing to prove. Hence we assume true for m-1.
Now, set all partial derivities of f of order for
Set is not onto }. This is just the critical points.
Clearly
We will show by backwards induction that
Comment:
We have not actually defined the measure . We use it merely to denote that has measure zero, a concept that we DID define.
Claim 1
has measure 0.
Proof
W.L.O.G (without loss of generality) we can assume n=1. Intuitively this is reasonable as in lower dimensions the theorem is harder to prove; indeed, a set of size in 1D becomes a smaller set of size in 2D etc. More precisely, for , . Applying the proposition that if A is of measure zero in then is measure zero in we now see that assuming n=1 is justified.
Reminder
Taylor's Theorem: for smooth enough and some then for some t between x and .
For all but the last term vanishes and so we can conclude that f(x) is bounded by a constant times .
Now let us consider a box B in containing a section of . We divide B into boxes of side .
By Taylor's Theorem, of an interval of length where the constant is determined by Taylor's Theorem. Call this interval
Hence,
But which tends to zero as tends to infinity.
Q.E.D for Claim 1
Claim 2
has measure zero for . We just proved this for k=m.
Now, W.L.O.G. is the empty set. If not, just consider which is still a manifold as is closed (as it is determined by the "closed" condition that a determinant equals zero)
So, there is some kth derivative g of f such that .
So but is at least locally a manifold of dimension 1 less. So, which has measure zero due to our induction hypothesis.
Q.E.D for Claim 2
Claim 3
is of measure zero.
Recall is defined differently from the and so requires a different technique to prove.
W.L.O.G. lets assume that is the empty set. So, some derivative of f is not zero. W.L.O.G. is non zero near some point p. We can simply move to a coordinate system where this is true.
The idea here is to prove that the intersection with any "slice" has measure zero where we will then invoke a theorem that will claim everything has measure zero.
So, let U be an open neighborhood of a point . Consider and let be onto. Using our previous theorem for the local structure of such a submersion W.L.O.G. let us assume via . That is, .
Our differential df then is just the matrix whose first row consists of . Then df is onto if the submatrix consisting of all but the first row and first column is invertible.
For notational convenience let us say .
Now define Also lets denote "critical points of f by CP(f) and "critical values of f" by CV(f)
Claim 4
The
.
But has measure zero by our induction.
Lemma 1
If is closed and has then .
Proof
Note: We prove this significantly differently then in Bredon
Sublemma
If for an open U cover for a closed A then such that
Indeed, let be then d is a continuous function of a compact set and so obtains a minimum and since d>0 then . But this works for the claim. Q.E.D
The rest of the proof of Lemma 1, and of Sard's Theorem will be left until next class



![{\displaystyle t\in [0,\pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8115ef0db1f941740f8a191359e5d01709c0df36)





![{\displaystyle C+C=[0,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b9786e2626f1ad2cf2cd7548bc62c8a144e91e1)









































































