0708-1300/Class notes for Tuesday, January 22
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pictures for a Van-Kampen Computation
In[1]:=
|
<< KnotTheory`
|
Loading KnotTheory` version of January 13, 2008, 20:30:12.1353.
Read more at http://katlas.org/wiki/KnotTheory.
In[2]:=
|
TubePlot[TorusKnot[8, 3]]
|
Out[2]=
|
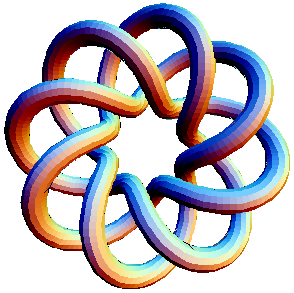
|
In[3]:=
|
TC[r1_, t1_,r2_,t2_ ] := {
(r1 +r2 Cos[2Pi t2])Cos[2Pi t1],
(r1 +r2 Cos[2Pi t2])Sin[2Pi t1],
r2 Sin[2Pi t2]
};
|
In[4]:=
|
InflatedTorus[p_, q_, b_] := ParametricPlot3D[
TC[
2, p t - q s,
1 + b(p^2 + q^2)s(1 - (p^2 + q^2)s), q t + p s
],
{t, 0, 1}, {s, 0, 1/(p^2 + q^2)},
PlotPoints -> {6(p^2 + q^2) + 1, 7},
DisplayFunction -> Identity
];
|
In[5]:=
|
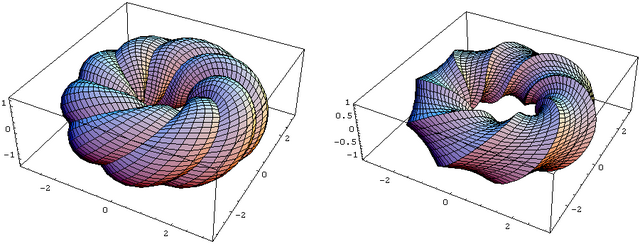
GraphicsArray[{{InflatedTorus[3,8,1], InflatedTorus[3,8,-1]}}]
|
Out[5]=
|
|
Typed Notes
First Hour
Today's Agenda:
1) More Examples of Van-Kampen Theorem
2) More Diagrams
3) Proof of Van-Kampen (was not done)
We began by recalling the examples from last class. I will not repeat that here, merely making a few additional comments that came out:
Notation:
Technically, is poor notion as it implies that knowledge of A, B and H is sufficient to construct . In fact, we ALSO need to know the maps from H into A and B respectively in order for to be defined.
Aside
Last class we simply wrote down the schematic for the two holed torus as an octagon with the identifications on the edges given last class. We now consider how one arrives at this schematic.
To create the two holed torus one begins with two tori. One then cuts out a small open disk from each torus and then glues the two boundaries together. Let us consider what this looks like when considering a torus as the normal schematic with a square in the plane with the normal identification of the sides. Removing an open disk is equivalent to removing the inside of a loop starting at one of the corners and finishing at that same corner. This is equivalent to making a pentagon with sides where c is the added edge.
Consider two such pentagons, gluing along the edge c forms precisely the octagon we had for the two holed torus last class.
Proposition
Letting denote the g holed torus, then
(Note, I used the symbol to as the normal \ncong command doesn't seem to work. Take its meaning in context.)
Aside: Consider a functor from the category of groups to the category of Abelian groups via
If we have a (homo)morphism from then the functor takes and yields a map such that everything commutes.
Hence we know that
Of course, we need to know that in fact if
As such, since the abelianizations are not isomorphic,neither are the original groups and the spaces themselves are not homeomorphic.
Example
is of the space which can be written as a disk with two antipodal points on the boundary circle on it with the identification that the top path a (going clockwise along the boundary) is glued to the bottom path (also going clock wise). But of this is just
Claim:
Puncturing an n-manifold, , does not change . I.e., if then
Proof:
Let
= a coordinate patch about p.
Then
If n=3, as we have computed before.
Hence,
Now,
Continuing inductively the theorem holds for all n.
Aside:
If X is connected and then . I.e., it does not matter which base point we choose in a connected space, the fundamental group is invariant of this.
Proof
Consider a path from to . The returning path is denoted
Consider a loop from called .
Then get a loop from via
Similarly about
Considering the composition we get .
Second Hour
Claim
is the union (with common boundary) of two solid tori
The natural way to add two tori with common boundary would be two glue the boundaries of two disks (making ) together for each angle going around the torus thus yielding . Clearly this is not the same as as the fundamental groups differ.
Instead consider the following description. Look at a torus in the zx plane, this looks like two disks with the z axis in between them such that rotating these two disks about the z axis will yield the torus.
Lets now add in the second torus into this picture. We first draw a horizontal line between the two disks. We then "blow" up from beneath so the horizontal line is slightly curved. We imagine continuing to blow yielding larger and larger loops between the two disks until it "pops" forming the pure horizontal line consisting of the loop at infinity. Do the same for the bottom. Hence, the boundaries of the two tori drawn this way clearly are the same, and between the two cover the entire zx plane (and "point at infinity). Rotating this picture about the z axis yields all of S^1 as the union of these two sets.
Claim:
= the normal solid torus thickened a bit and under yields
= the other solid torus, also thickened a bit, under yields is a normal torus only with slightly thick walls opposed to infinitely thin ones (homotopically the same)
So,
So,
However, we still need to describe and
Do do this let me describe a,b, and explicitly.
Considering the description of the two tori given above, we let a go around the outside of one of the two disks in the plane and b go from a point on the boundary of the same disk, following the rotation about the z axis, to a point on the boundary of the other dis. is similar to b, but thought of as being on the boundary of the OTHER torus. consists of the path along the z axis.
Hence,
(as it is contractible)
Hence,
Hence,
Example
Define the "Torus knot " where p and q are relatively prime integers. The knot is given above. We can think of this in the following ways:
1) is the knot that wraps around the torus p times one way and q times the other way.
2) Formally, let be standard embedding of a torus. Let be
Then is
3) Recall that the torus can be thought of as the image of the mapping
Consider the rectangle in the real plane: ([0,p],[0,q]) and consider the path which is the diagonal line from the corner (0,0) to the corner (p,q)
No two points on this line are the same under the mapping down to the torus. If they were, then and would be integers and hence would be the slope of the line. But the slope of the line is q/p which is already in lowest common terms by assumption.
Lets compute the fundamental group of the compliment of the torus knot.
: inflated bagel, constrained by
: inflated bubble constrained by
(See top of page for pictures)
The intersection looks somewhat like a belt. It has some thickness to it and is wrapped around the torus, eventually forming a loop. Hence it looks like a squashed disk cross a circle. Hence, under this is just where is the path parallel to
We thus get the maps,
Hence,
Thus,
Diagrams:
Recall our diagram from last class:
can be defined as the object such that the above diagram commutes and should the following commute:
Then there is a unique map between and Y such that the composed diagram commutes.
Indeed, the same is true for general categories.
For
commuting, P is defined as an object such that if also
were to commute then there is a unique morphism from P to Q such that the composed diagram computes.
In the category of groups, this "pushforward" P is unique and is isomorphic to






























































![{\displaystyle \gamma :[0,1]\rightarrow S^{1}\times S^{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b63509a956c620f137cbb46c41e7823d7c79b2)

















