| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 11
|
About, Tue, HW1, Putnam, Thu
|
| 2
|
Sep 18
|
Tue, HW2, Thu
|
| 3
|
Sep 25
|
Tue, HW3, Photo, Thu
|
| 4
|
Oct 2
|
Tue, HW4, Thu
|
| 5
|
Oct 9
|
Tue, HW5, Thu
|
| 6
|
Oct 16
|
Why?, Iso, Tue, Thu
|
| 7
|
Oct 23
|
Term Test, Thu (double)
|
| 8
|
Oct 30
|
Tue, HW6, Thu
|
| 9
|
Nov 6
|
Tue, HW7, Thu
|
| 10
|
Nov 13
|
Tue, HW8, Thu
|
| 11
|
Nov 20
|
Tue, HW9, Thu
|
| 12
|
Nov 27
|
Tue, HW10, Thu
|
| 13
|
Dec 4
|
On the final, Tue, Thu
|
| F
|
Dec 11
|
Final: Dec 13 2-5PM at BN3, Exam Forum
|
| Register of Good Deeds
|

Add your name / see who's in!
|
| edit the panel
|
|
Our remaining goal for this semester is to study the following theorem:
Theorem. Let  be an
be an  matrix (with entries in some field
matrix (with entries in some field  ) and let
) and let  be the characteristic polynomial of
be the characteristic polynomial of  . Assume
. Assume  has
has  distinct roots
distinct roots  , that is,
, that is,  has
has  distinct eigenvalues
distinct eigenvalues  , and let
, and let  be corresponding eigenvectors, so that
be corresponding eigenvectors, so that  for all
for all  . Let
. Let  be the diagonal matrix that has
be the diagonal matrix that has  through
through  on its main diagonal (in order) and let
on its main diagonal (in order) and let  be the matrix whose columns are these eigenvectors:
be the matrix whose columns are these eigenvectors:  . Then
. Then  is invertible and the following equalities hold:
is invertible and the following equalities hold:
 and
and  .
.- For any positive integer
 we have
we have  and
and  .
.
- Likewise if
 and
and  then
then  and
and  .
.
Order of the proceedings.
- Assuming P is invertible, a proof of 1.
- Proof of 2.
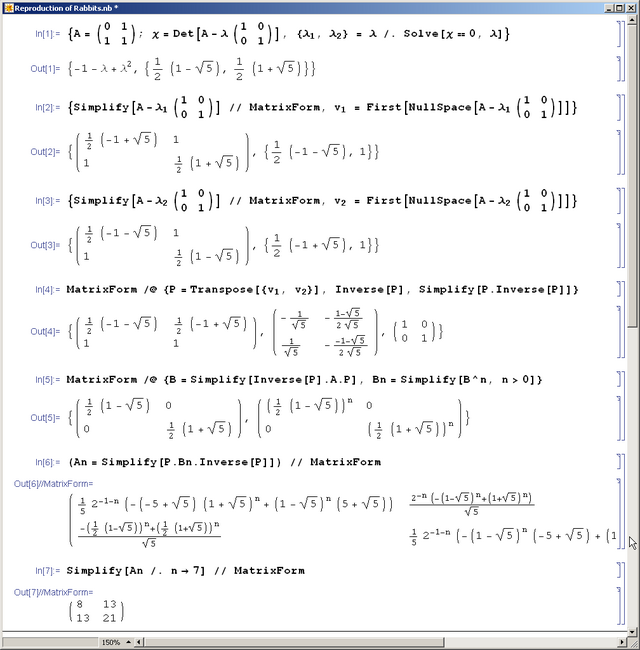
- Example - the "reproduction of rabbits" matrix
 (see the mathematica session below).
(see the mathematica session below).
- Discussion of 3.
- The relationship with linear transformations and changes of basis.
 thorough
thorough  form a basis and
form a basis and  is invertible.
is invertible.