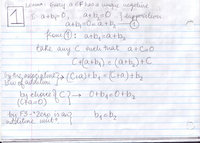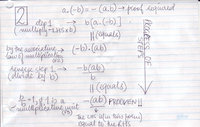| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 11
|
About, Tue, HW1, Putnam, Thu
|
| 2
|
Sep 18
|
Tue, HW2, Thu
|
| 3
|
Sep 25
|
Tue, HW3, Photo, Thu
|
| 4
|
Oct 2
|
Tue, HW4, Thu
|
| 5
|
Oct 9
|
Tue, HW5, Thu
|
| 6
|
Oct 16
|
Why?, Iso, Tue, Thu
|
| 7
|
Oct 23
|
Term Test, Thu (double)
|
| 8
|
Oct 30
|
Tue, HW6, Thu
|
| 9
|
Nov 6
|
Tue, HW7, Thu
|
| 10
|
Nov 13
|
Tue, HW8, Thu
|
| 11
|
Nov 20
|
Tue, HW9, Thu
|
| 12
|
Nov 27
|
Tue, HW10, Thu
|
| 13
|
Dec 4
|
On the final, Tue, Thu
|
| F
|
Dec 11
|
Final: Dec 13 2-5PM at BN3, Exam Forum
|
| Register of Good Deeds
|

Add your name / see who's in!
|
| edit the panel
|
|
- PDF notes by User:Harbansb: September 12 Notes.
- If I have made an error in my notes, or you would like the editable OpenOffice file, feel free to e-mail me at harbansb@msn.com.
- September 12 Notes for re-uploading, please email at jeff.matskin@utoronto.ca
- PDF notes by User:Alla: Week 1 Lecture 1 notes
- Below are a couple of lemmata critical to the derivation we did in class - the Professor left this little work to the students:
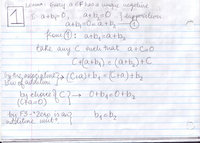
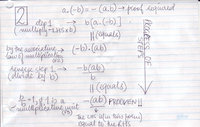
Notes
The Real Numbers
The Real Numbers are a set (denoted by  ) along with two binary operations: + (plus) and · (times) and two special elements: 0 (zero) and 1 (one), such that the following laws hold true:
) along with two binary operations: + (plus) and · (times) and two special elements: 0 (zero) and 1 (one), such that the following laws hold true:
 :
:  we have
we have  and
and  (The Commutative Laws)
(The Commutative Laws)
 :
:  we have
we have  and
and  (The Associative Laws)
(The Associative Laws)
 :
:  is an additive unit and
is an additive unit and  is a multiplicative unit (The Existence of Units/Identities)
is a multiplicative unit (The Existence of Units/Identities)
 :
: 
This is incomplete.