© | Dror Bar-Natan: Classes: 2013-14: AKT:  < > 

AKT-140321 Video

width: 400 720 ogg/AKT-140321_400.ogg orig/AKT-140321.MOD
Videography by Iva Halacheva troubleshooting

pop-out / sync handout

Notes on AKT-140321:    [edit, refresh]

refresh
panel Managed by dbnvp: Click the "h:mm:ss" links on the right panel to jump to a specific video time.
0:25:33 [add] The Faddeev-Popov determinant formula.
0:31:06 [add] Faddeev-Popov in the case of rotations on ${\mathbb R}^2$.
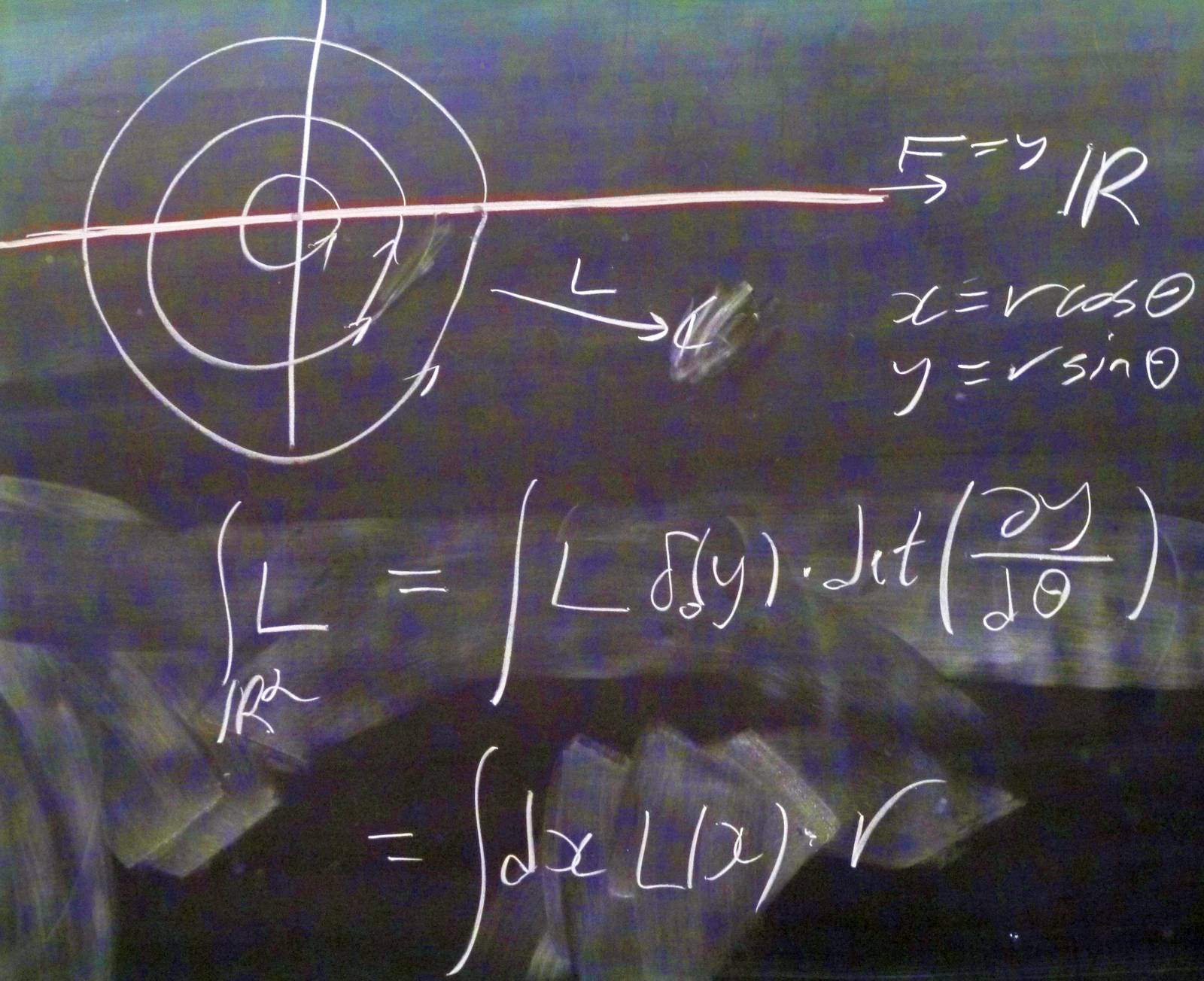
0:31:32 [add] Handout view 2: R^n definitions
0:31:43 [add] Handout view 5: The Fourier Transform
0:31:49 [add] Handout view 10: Unmarked Feynman Diagrams
0:31:55 [add] Handout view 13: Second wish
0:36:17 [add] Handout view 14: Perturbing determinants
0:36:20 [add] Handout view 13: Second wish
0:36:45 [add] Handout view 14: Perturbing determinants
0:41:54 [add] $\det(Q+\epsilon P)$.
0:48:35 [add] Handout view 15: Expanding 2nd wish
0:50:11 [add] Handout view 14: Perturbing determinants
0:51:54 [add] $\det(Q+\epsilon P)$ (2).
0:52:11 [add] Handout view 15: Expanding 2nd wish
0:52:44 [add] Handout view 16: 1st diagrammatics
0:53:16 [add] Handout view 18: Berezin
0:53:21 [add] Handout view 19: Interior multiplication